题目内容
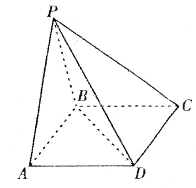
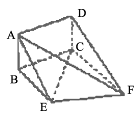
如图,四棱锥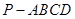 的底面
的底面 是矩形,
是矩形,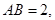
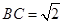 ,且侧面
,且侧面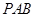 是正三角形,平面
是正三角形,平面 平面
平面 ,
,
(Ⅰ)求证: ;
;
(Ⅱ)在棱 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角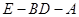 的大小为45°.若存在,试求
的大小为45°.若存在,试求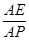 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
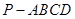 的底面
的底面 是矩形,
是矩形,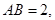
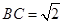 ,且侧面
,且侧面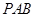 是正三角形,平面
是正三角形,平面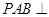 平面
平面 ,
,
(Ⅰ)求证:
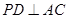 ;
;(Ⅱ)在棱
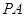 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角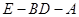 的大小为45°.若存在,试求
的大小为45°.若存在,试求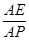 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(1)见解析;(2)45°.
第一问先利用取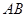 中点
中点 ,由
,由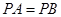 ,得
,得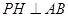 ,又平面
,又平面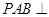 平面
平面 ,且平面
,且平面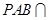 平面
平面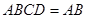 ,所以
,所以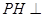 平面
平面 ,然后以
,然后以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系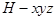 ,结合向量的数量积公式
,结合向量的数量积公式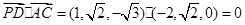 得到证明。
得到证明。
第二问中,假设在棱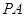 上存在一点
上存在一点 ,不妨设
,不妨设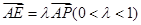 ,
,
则点 的坐标为
的坐标为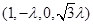 则得到平面
则得到平面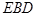 的一个法向量
的一个法向量 .,
.,
又面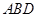 的法向量可以是
的法向量可以是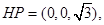 向量的夹角公式,表示出二面角,从而解得。
向量的夹角公式,表示出二面角,从而解得。
取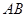 中点
中点 ,则由
,则由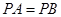 ,得
,得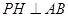 ,又平面
,又平面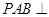 平面
平面 ,且平面
,且平面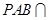 平面
平面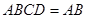 ,所以
,所以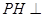 平面
平面 .以
.以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系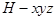 (如图).则
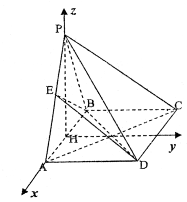
(如图).则 ……………………………2分
……………………………2分
(Ⅰ)证明:∵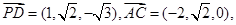
……………………………………………………………………4分
∴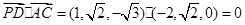 ,
,
∴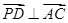 ,即
,即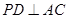 .…………………………………6分
.…………………………………6分
(Ⅱ)假设在棱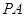 上存在一点
上存在一点 ,不妨设
,不妨设
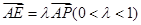 ,
,
则点 的坐标为
的坐标为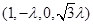 ,……………………………8分
,……………………………8分
∴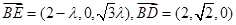
设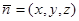 是平面
是平面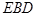 的法向量,则
的法向量,则

不妨取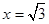 ,则得到平面
,则得到平面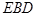 的一个法向量
的一个法向量 .…………………10分
.…………………10分
又面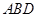 的法向量可以是
的法向量可以是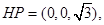
要使二面角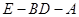 的大小等于45°,
的大小等于45°,
则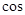 45°=
45°=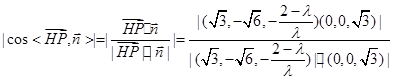
可解得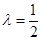 ,即
,即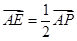
故在棱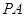 上存在点
上存在点 ,当
,当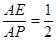 时,使得二面角
时,使得二面角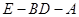 的大小等于45°. ………12分
的大小等于45°. ………12分
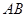 中点
中点 ,由
,由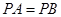 ,得
,得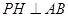 ,又平面
,又平面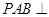 平面
平面 ,且平面
,且平面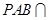 平面
平面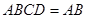 ,所以
,所以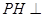 平面
平面 ,然后以
,然后以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系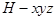 ,结合向量的数量积公式
,结合向量的数量积公式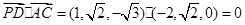 得到证明。
得到证明。第二问中,假设在棱
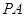 上存在一点
上存在一点 ,不妨设
,不妨设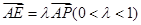 ,
,则点
 的坐标为
的坐标为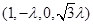 则得到平面
则得到平面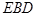 的一个法向量
的一个法向量 .,
.,又面
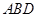 的法向量可以是
的法向量可以是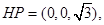 向量的夹角公式,表示出二面角,从而解得。
向量的夹角公式,表示出二面角,从而解得。取
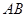 中点
中点 ,则由
,则由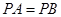 ,得
,得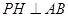 ,又平面
,又平面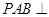 平面
平面 ,且平面
,且平面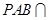 平面
平面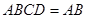 ,所以
,所以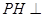 平面
平面 .以
.以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系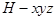 (如图).则
(如图).则 ……………………………2分
……………………………2分
(Ⅰ)证明:∵
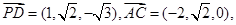
……………………………………………………………………4分
∴
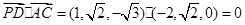 ,
,∴
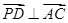 ,即
,即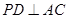 .…………………………………6分
.…………………………………6分(Ⅱ)假设在棱
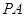 上存在一点
上存在一点 ,不妨设
,不妨设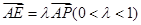 ,
,则点
 的坐标为
的坐标为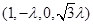 ,……………………………8分
,……………………………8分∴
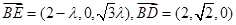
设
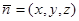 是平面
是平面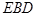 的法向量,则
的法向量,则
不妨取
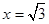 ,则得到平面
,则得到平面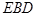 的一个法向量
的一个法向量 .…………………10分
.…………………10分又面
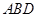 的法向量可以是
的法向量可以是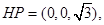
要使二面角
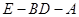 的大小等于45°,
的大小等于45°,则
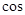 45°=
45°=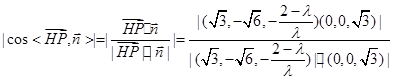
可解得
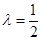 ,即
,即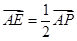
故在棱
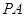 上存在点
上存在点 ,当
,当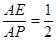 时,使得二面角
时,使得二面角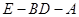 的大小等于45°. ………12分
的大小等于45°. ………12分
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
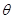 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.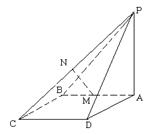
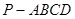 中,平面
中,平面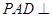 平面
平面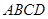 ,
,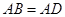 ,
,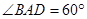 ,
, 、
、 分别是
分别是 、
、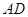 的中点。
的中点。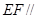 平面
平面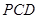 ;
;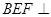 平面
平面 。(12分)
。(12分)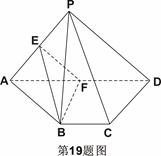
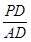 =
=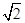 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.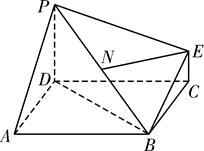
 BCF=
BCF=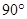 ,AD=
,AD=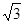 ,EF=2.
,EF=2.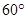 .
.
 是
是 的直径,点
的直径,点 是
是 重合),过动点
重合),过动点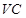 垂直于
垂直于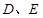 分别是
分别是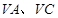 的中点,则下列结论错误的是
的中点,则下列结论错误的是 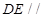 平面
平面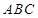
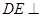 平面
平面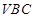
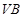
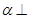 平面
平面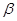 ,那么平面
,那么平面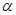 内一定存在直线平行于平面
内一定存在直线平行于平面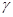 ,平面
,平面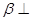 平面
平面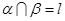 ,那么
,那么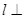 平面
平面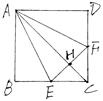
 平面EFG
平面EFG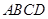 为矩形,且
为矩形,且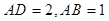 ,
,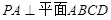 ,
,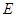 为
为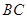 上的动点。
上的动点。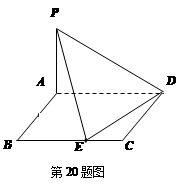
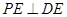 ;
;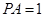 ,在线段
,在线段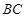 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角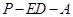 的平面角大小为
的平面角大小为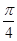 。试确定点E的位置。
。试确定点E的位置。