题目内容
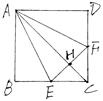
如图在四棱锥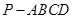 中,底面
中,底面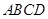 是菱形,
是菱形,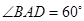 ,
,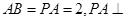 底面
底面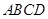 ,
,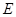 是
是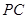 的中点,
的中点,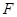 是
是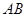 中点。
中点。
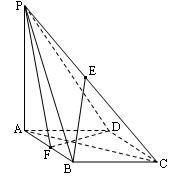
(1)求证: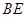 ∥平面
∥平面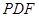 ;
;
(2)求证:平面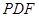 ⊥平面
⊥平面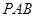 ;
;
(3)求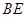 与平面
与平面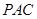 所成的角。
所成的角。
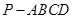 中,底面
中,底面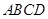 是菱形,
是菱形,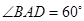 ,
,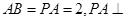 底面
底面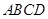 ,
,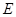 是
是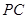 的中点,
的中点,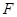 是
是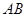 中点。
中点。
(1)求证:
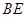 ∥平面
∥平面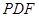 ;
;(2)求证:平面
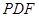 ⊥平面
⊥平面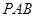 ;
;(3)求
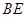 与平面
与平面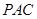 所成的角。
所成的角。解:(1)(2) 见解析
(3)直线BE与平面PAC所成的角为450
(3)直线BE与平面PAC所成的角为450
往往有两个中点时,考虑中位线,当两中点不能构成中位线时,考虑构造另一个中点,组成两对中位线。∵ PA⊥平面ABCD 则PA⊥平面ABCD内所有的直线,∴ DF⊥PA,再结合四边形ABCD是菱形,找到另一垂直条件。
(1)取PD中点为M,连ME,MF ∵ E是PC的中点
∴ ME是△PCD的中位线∴ ME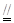
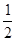 CD ∵ F是AB中点且由于ABCD是菱形,AB
CD ∵ F是AB中点且由于ABCD是菱形,AB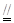 CD
CD
∴ ME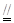 FB ∴ 四边形MEBF是平行四边形 …………2分
FB ∴ 四边形MEBF是平行四边形 …………2分
∴ BE∥MF …………………3分
∵ BE 平面PDF ,MF
平面PDF ,MF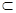 平面PDF ∴ BE∥平面PDF ………4分
平面PDF ∴ BE∥平面PDF ………4分
(2) ∵ PA⊥平面ABCD DF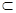 平面ABCD ∴ DF⊥PA……………5分
平面ABCD ∴ DF⊥PA……………5分
∵ 底面ABCD是菱形,∠BAD=600 ∴ △DAB为正△
∵ F是AB中点 ∴ DF⊥AB ……………6分
∵ PA、AB是平面PAB内的两条相交直线 ∴ DF⊥平面PAB ………7分
∵ DF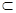 平面PDF ∴ 平面PDF⊥平面PAB ………………8分
平面PDF ∴ 平面PDF⊥平面PAB ………………8分
(3)连BD交AC与O、连EO ∵ 底面ABCD是菱形 ∴ BO⊥AC
∵ PA⊥平面ABCD BO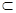 平面ABCD ∴ BO⊥PA
平面ABCD ∴ BO⊥PA
∵ PA、AC是平面PAC内的两条相交直线 ∴ BO⊥平面PAC …………9分
∴ EO是BE在平面PAC内的射影
∴ ∠BEO是BE与平面PAC所成的角 ………………10分
∵ O是AC、BD的中点 ∴ BO=1,EO是△PAC的中位线 ∴ EO=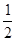 PA=1
PA=1
∴ 在直角△BEO中,tan∠BEO= ="1" ∴ ∠BEO=450
="1" ∴ ∠BEO=450
∴ 直线BE与平面PAC所成的角为450
(1)取PD中点为M,连ME,MF ∵ E是PC的中点
∴ ME是△PCD的中位线∴ ME
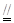
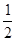 CD ∵ F是AB中点且由于ABCD是菱形,AB
CD ∵ F是AB中点且由于ABCD是菱形,AB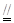 CD
CD∴ ME
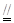 FB ∴ 四边形MEBF是平行四边形 …………2分
FB ∴ 四边形MEBF是平行四边形 …………2分∴ BE∥MF …………………3分
∵ BE
 平面PDF ,MF
平面PDF ,MF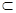 平面PDF ∴ BE∥平面PDF ………4分
平面PDF ∴ BE∥平面PDF ………4分(2) ∵ PA⊥平面ABCD DF
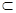 平面ABCD ∴ DF⊥PA……………5分
平面ABCD ∴ DF⊥PA……………5分∵ 底面ABCD是菱形,∠BAD=600 ∴ △DAB为正△
∵ F是AB中点 ∴ DF⊥AB ……………6分
∵ PA、AB是平面PAB内的两条相交直线 ∴ DF⊥平面PAB ………7分
∵ DF
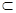 平面PDF ∴ 平面PDF⊥平面PAB ………………8分
平面PDF ∴ 平面PDF⊥平面PAB ………………8分(3)连BD交AC与O、连EO ∵ 底面ABCD是菱形 ∴ BO⊥AC
∵ PA⊥平面ABCD BO
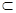 平面ABCD ∴ BO⊥PA
平面ABCD ∴ BO⊥PA∵ PA、AC是平面PAC内的两条相交直线 ∴ BO⊥平面PAC …………9分
∴ EO是BE在平面PAC内的射影
∴ ∠BEO是BE与平面PAC所成的角 ………………10分
∵ O是AC、BD的中点 ∴ BO=1,EO是△PAC的中位线 ∴ EO=
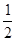 PA=1
PA=1∴ 在直角△BEO中,tan∠BEO=
 ="1" ∴ ∠BEO=450
="1" ∴ ∠BEO=450∴ 直线BE与平面PAC所成的角为450

练习册系列答案
相关题目

 的正方形,且PD=
的正方形,且PD=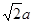 .
.
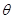 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.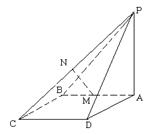
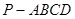 中,平面
中,平面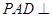 平面
平面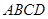 ,
,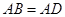 ,
,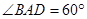 ,
,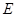 、
、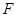 分别是
分别是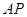 、
、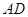 的中点。
的中点。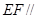 平面
平面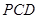 ;
;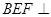 平面
平面 。(12分)
。(12分)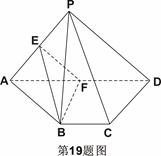
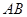 是
是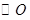 的直径,点
的直径,点 是
是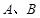 重合),过动点
重合),过动点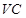 垂直于
垂直于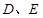 分别是
分别是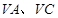 的中点,则下列结论错误的是
的中点,则下列结论错误的是 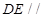 平面
平面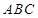
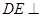 平面
平面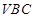
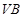
 ,
,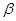 是两个不同的平面,
是两个不同的平面,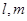 是两条不重合的直线,下列命题中正确的是( )
是两条不重合的直线,下列命题中正确的是( )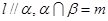 ,则
,则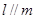 .
.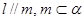 ,则
,则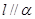 .
.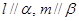 ,且
,且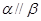 ,则
,则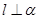 ,
,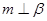 且
且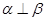 ,则
,则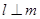 .
. 中,
中, ,
, ,点
,点 在棱
在棱 上移动,问
上移动,问 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.
 平面EFG
平面EFG