题目内容
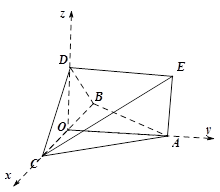
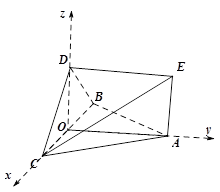
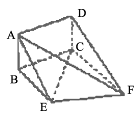
如图,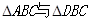 均是边长为2的等边三角形,且它们所在平面互相垂直,
均是边长为2的等边三角形,且它们所在平面互相垂直,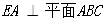 ,
,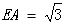 .
.
(1) 求证: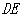 ||
|| 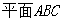
(2) 求二面角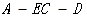 的余弦值。.
的余弦值。. 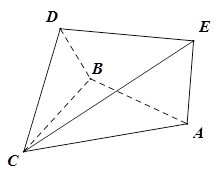
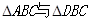 均是边长为2的等边三角形,且它们所在平面互相垂直,
均是边长为2的等边三角形,且它们所在平面互相垂直,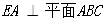 ,
,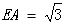 .
.(1) 求证:
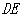 ||
|| 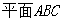
(2) 求二面角
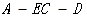 的余弦值。.
的余弦值。. 
(1)见解析.(2)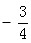 .
.
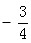 .
.本试题主要考查了立体几何中线面平行而后二面角的求解的运用。第一问中,利用取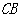 的中点
的中点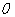 ,连接
,连接 ,
,

 是边长为2的等边三角形
是边长为2的等边三角形 

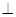
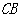 且
且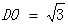
又
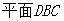
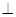
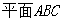


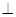

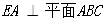 ,
,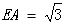

 ||
||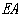 ,
, =
=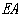
 四边形
四边形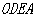 为矩形
为矩形

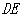 ||
||
得到先面平行。
第二问中,建系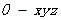 如图所示:易知,
如图所示:易知,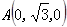 ,
,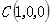 ,
,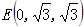 ,
,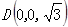
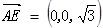 ,
,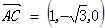 ,
,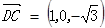 ,
,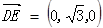 ,利用法向量来求解二面角的大小。
,利用法向量来求解二面角的大小。
解:(1)取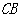 的中点
的中点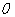 ,连接
,连接 ,
,

 是边长为2的等边三角形
是边长为2的等边三角形 

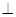
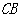 且
且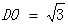
又
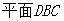
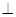
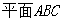


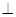
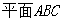

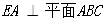 ,
,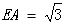

 ||
||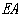 ,
, =
=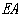
 四边形
四边形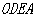 为矩形
为矩形

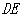 ||
||
又
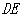
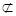
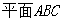 ,
,
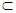
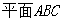

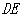 ||
|| 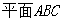 ……………………………………6分
……………………………………6分
(2)建系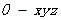 如图所示:易知,
如图所示:易知,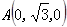 ,
,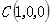 ,
,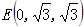 ,
,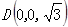
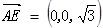 ,
,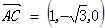 ,
,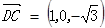 ,
, ………………………7分
………………………7分
设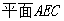 的法向量
的法向量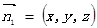
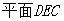 的法向量
的法向量 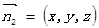

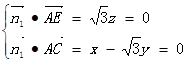

令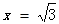 得
得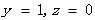
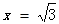 得
得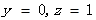

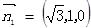
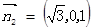 ………………………. .10分
………………………. .10分
 …………………………………………11分
…………………………………………11分
由图形可知,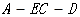 钝二面角,故二面角
钝二面角,故二面角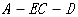 的余弦值为
的余弦值为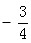 ……….12分
……….12分
 的中点
的中点 ,连接
,连接 ,
,

 是边长为2的等边三角形
是边长为2的等边三角形 

 且
且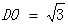
又

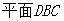
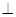
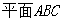


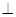
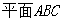

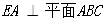 ,
,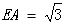

 ||
||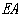 ,
, =
=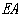
 四边形
四边形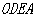 为矩形
为矩形
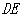 ||
||
得到先面平行。
第二问中,建系
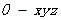 如图所示:易知,
如图所示:易知,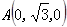 ,
,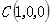 ,
,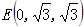 ,
,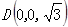
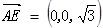 ,
,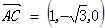 ,
,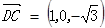 ,
,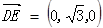 ,利用法向量来求解二面角的大小。
,利用法向量来求解二面角的大小。
解:(1)取
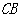 的中点
的中点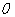 ,连接
,连接 ,
,

 是边长为2的等边三角形
是边长为2的等边三角形 

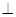
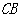 且
且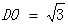
又

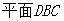
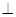
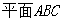


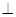
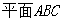

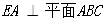 ,
,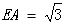

 ||
||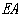 ,
, =
=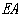
 四边形
四边形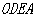 为矩形
为矩形
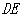 ||
||
又

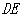
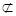
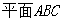 ,
,
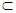
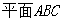

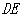 ||
|| 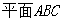 ……………………………………6分
……………………………………6分(2)建系
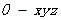 如图所示:易知,
如图所示:易知,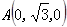 ,
,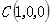 ,
,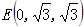 ,
,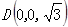
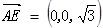 ,
,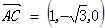 ,
,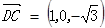 ,
,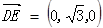 ………………………7分
………………………7分
设
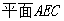 的法向量
的法向量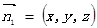
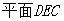 的法向量
的法向量 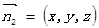

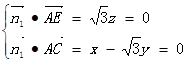

令
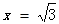 得
得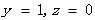
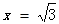 得
得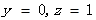

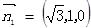
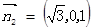 ………………………. .10分
………………………. .10分 …………………………………………11分
…………………………………………11分由图形可知,
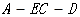 钝二面角,故二面角
钝二面角,故二面角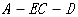 的余弦值为
的余弦值为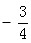 ……….12分
……….12分
练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
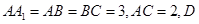 是
是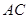 中点.
中点.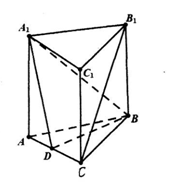
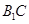 //平面
//平面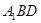 ;
;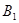 到平面
到平面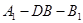 的余弦值.
的余弦值.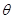 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.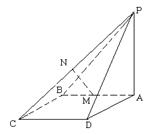
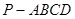 中,平面
中,平面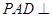 平面
平面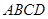 ,
,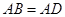 ,
,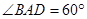 ,
,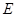 、
、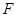 分别是
分别是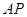 、
、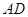 的中点。
的中点。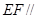 平面
平面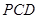 ;
;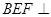 平面
平面 。(12分)
。(12分)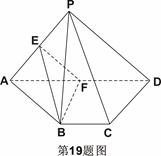
 BCF=
BCF=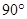 ,AD=
,AD=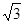 ,EF=2.
,EF=2. .
.
 ,
, 是两个不同的平面,
是两个不同的平面,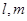 是两条不重合的直线,下列命题中正确的是( )
是两条不重合的直线,下列命题中正确的是( )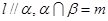 ,则
,则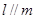 .
.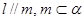 ,则
,则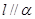 .
.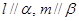 ,且
,且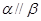 ,则
,则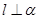 ,
,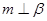 且
且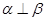 ,则
,则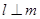 .
.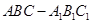 中,
中,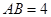 ,
,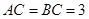 ,
,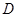 为
为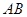 的中点。(Ⅰ)求点C到平面
的中点。(Ⅰ)求点C到平面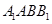 的距离;(Ⅱ)若
的距离;(Ⅱ)若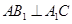 ,求二面角
,求二面角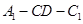 的平面角的余弦值。
的平面角的余弦值。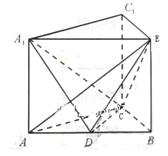
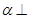 平面
平面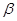 ,那么平面
,那么平面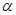 内一定存在直线平行于平面
内一定存在直线平行于平面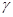 ,平面
,平面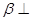 平面
平面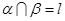 ,那么
,那么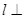 平面
平面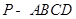 中,
中,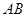 //
//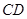 ,
,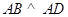 ,
, ,
,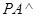 平面
平面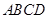 ,
,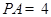 .
. 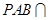 平面
平面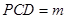 ,求证:
,求证: ;
; 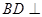 平面
平面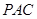 ;
; 为线段
为线段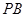 上一点,且直线
上一点,且直线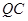 与平面
与平面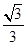 ,求
,求 的值.
的值.