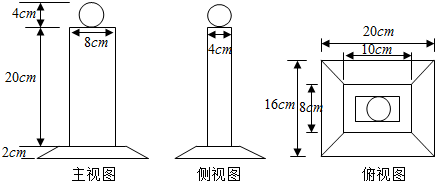
题目内容
7.设函数f(x)=$\left\{{\begin{array}{l}{{{log}_{\frac{1}{2}}}x}&{x>0}\\{x+6}&{x≤0}\end{array}}$,则f(f(-4))的值是-1.分析 直接利用分段函数的解析式,由里及外逐步求解即可.
解答 解:函数f(x)=$\left\{{\begin{array}{l}{{{log}_{\frac{1}{2}}}x}&{x>0}\\{x+6}&{x≤0}\end{array}}$,则f(f(-4))=f(-4+6)=f(2)=${log}_{\frac{1}{2}}2$=-1.
故答案为:-1.
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
18.设a=log0.32,b=log32,c=20.3,则这三个数的大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
2.下列函数中,为奇函数的是( )
| A. | y=2x+$\frac{1}{2^x}$ | B. | y=x,x∈(0,1] | C. | y=x3+x | D. | y=x3+1 |
12.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
| A. | y=x3 | B. | $y=|{log_2^{\;}x}|$ | C. | y=2|x| | D. | y=-x2+1 |