题目内容
15.在边长为2的菱形ABCD中,∠BAD=$\frac{2π}{3}$,$\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AD}$,则$\overrightarrow{PB}$$•\overrightarrow{PD}$的值为$-\frac{12}{9}$.分析 由题意画出图形,利用已知及平面向量基本定理把$\overrightarrow{PB}、\overrightarrow{PD}$用向量$\overrightarrow{AB}、\overrightarrow{AD}$表示,然后展开数量积运算得答案.
解答  解:如图,$|\overrightarrow{AB}|=|\overrightarrow{AD}|=2$,$∠A=\frac{2π}{3}$,
解:如图,$|\overrightarrow{AB}|=|\overrightarrow{AD}|=2$,$∠A=\frac{2π}{3}$,
$\overrightarrow{PB}$$•\overrightarrow{PD}$=($\overrightarrow{PA}+\overrightarrow{AB}$)•$\frac{2}{3}\overrightarrow{AD}$
=($-\frac{1}{3}\overrightarrow{AD}$$+\overrightarrow{AB}$)•$\frac{2}{3}\overrightarrow{AD}$
=$-\frac{2}{9}|\overrightarrow{AD}{|}^{2}$+$\frac{2}{3}\overrightarrow{AB}•\overrightarrow{AD}$=$-\frac{2}{9}×4+\frac{2}{3}×2×2×cos\frac{2π}{3}$=$-\frac{8}{9}+\frac{8}{9}×(-\frac{1}{2})=-\frac{12}{9}$.
故答案为:$-\frac{12}{9}$.
点评 本题考查平面向量的数量积运算,训练了平面向量基本定理的应用,是中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
10.函数f(x)=ln$\frac{3x}{2}-\frac{2}{x}$,则函数f(x)的零点所在区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
20.设D为△ABC所在平面内一点,$\overrightarrow{AD}=2\overrightarrow{CD}$,则( )
| A. | $\overrightarrow{BD}=-\overrightarrow{BA}+2\overrightarrow{BC}$ | B. | $\overrightarrow{BD}=2\overrightarrow{BA}-\overrightarrow{BC}$ | C. | $\overrightarrow{BD}=\overrightarrow{BA}+2\overrightarrow{BC}$ | D. | $\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BA}+\frac{2}{3}\overrightarrow{BC}$ |
4.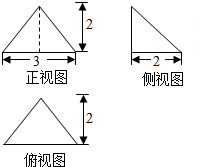 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )
 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )| A. | 6 | B. | 18 | C. | 8+3$\sqrt{2}$ | D. | 3+4$\sqrt{13}$ |
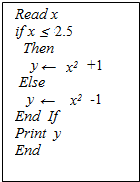 若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.
若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.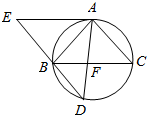 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.