题目内容
17.已知函数f(x)=$\frac{{{a^x}-1}}{{{a^x}+1}}$(a>0,a≠1)(1)判断函数的奇偶性,并证明;
(2)求该函数的值域;
(3)判断f(x)在R上的单调性,并证明.
分析 (1)函数f(x)的定义域为R,计算f(-x),与±f(x)的关系,即可判断出奇偶性;
(2)由f(x)=1-$\frac{2}{{a}^{x}+1}$,设t=ax,则t>0,$y=1-\frac{2}{t+1}$,利用函数的单调性即可得出值域.
(3)设x1<x2,f(x)=1-$\frac{2}{{a}^{x}+1}$,通过作差、分类讨论即可得出.
解答 解:(1)函数f(x)的定义域为R,f(-x)=$\frac{{a}^{-x}-1}{{a}^{-x}+1}$=$\frac{1-{a}^{x}}{1+{a}^{x}}$=-f(x),
∴f(x)为奇函数.
(2)∵f(x)=1-$\frac{2}{{a}^{x}+1}$,
设t=ax,则t>0,
$y=1-\frac{2}{t+1}$,
∴该函数的值域为(-1,1),
(3)设x1<x2,f(x)=1-$\frac{2}{{a}^{x}+1}$,
则f(x1)-f(x2)=$(1-\frac{2}{{a}^{{x}_{1}}+1})-(1-\frac{2}{{a}^{{x}_{2}}+1})$=$\frac{2({a}^{{x}_{1}}-{a}^{{x}_{2}})}{({a}^{{x}_{1}}+1)({a}^{{x}_{2}}+1)}$,
若a>1,则$0<{a}^{{x}_{1}}<{a}^{{x}_{2}}$,∴${a}^{{x}_{1}}<{a}^{{x}_{2}}$,${a}^{{x}_{1}}+1>$0,${a}^{{x}_{2}}+1$>0.
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在R上是增函数.
若0<a<1,则同理可证明f(x)在R上是增函数.
点评 本题考查了函数的奇偶性与单调性,考查了推理能力与计算能力,属于中档题.

| A. | -sin2x | B. | -2cosx | C. | 2sinx | D. | 2cosx |
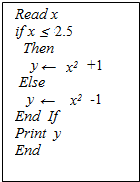 若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.
若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.