题目内容
【题目】某教育部门为了了解某地区高中学生每周的课外羽毛球训练的情况，随机抽取了该地区50名学生进行调查，其中男生25人．将每周课外训练时间不低于8小时的学生称为“训练迷”，低于8小时的学生称为“非训练迷”．已知“训练迷”中有15名男生．根据调查结果绘制的学生每周课外训练时间的频率分布直方图（时间单位为小时）如图所示．
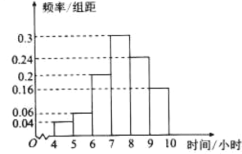
（1）根据图中数据估计该地区高中学生每周课外训练的平均时间（说明：同一组中的数据用该组区间的中间值作代表）；
（2）根据已知条件完成下面的
列联表，并判断是否有99.5%的把握认为“训练迷”与性别有关？
非训练迷 | 训练迷 | 合计 | |
男 | |||
女 | |||
合计 |
（3）将每周课外训练时间为4-6小时的称为“业余球迷”，已知调查样本中，有3名“业余球迷”是男生，若从“业余球迷”中任意选取2人，求至少有1名男生的概率．
附：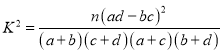
．
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
【答案】（1）7.62小时；（2）列联表详见解析，有99.5%的把握认为“训练迷”与性别有关；（3）
．
【解析】
（1）取中点直接代入计算即可.
（2）分别计算出“训练迷”中的男生和女生人数，简单计算，并填写表格，然后根据
公式，计算，最后比较数据，可得结果.
（3）将“业余球迷”中男生、女生分别作好标记，并使用列举法，得到所有可能结果，然后计算“至少有一名男生”的个数，最后根据古典概型可得结果.
解：（1）设该地区高中学生每周课外训练的平均时间为
，
则
（小时）
故答案为：7.62小时．
（2）因为每周训练时间不低于8小时的频率为
，
所以“训练迷”的学生人数为
．故根据已知条件完成的
列联表如下：
非训练迷 | 训练迷 | 合计 | |
男 | 10 | 15 | 25 |
女 | 20 | 5 | 25 |
合计 | 30 | 20 | 50 |
根据公式得，的观测值
，
故有99.5%的把握认为“训练迷”与性别有关．
（3）由频率分布直方图可知，“业余球迷”有
人，其中男生3人，记作a，b，c；女生2人，记作X，
，
，
，
，
，
，
，
，
，
，共10种；
用M表示事件：从“业余球迷”中任意选取2人，至少有1名男生，
显然事件M的基本事件为：，，，，，，，，，共9种．
故由古典概型的概率公式，得
故答案为：．
