题目内容
【题目】若![]() ,不等式
,不等式![]() 恒成立,则正实数
恒成立,则正实数![]() 的取值范围是_____.
的取值范围是_____.
【答案】![]()
【解析】
由题意可得(eλx![]() )min≥0,设f(x)=eλx
)min≥0,设f(x)=eλx![]() ,x>0,求出导数和单调区间、极小值点m和最小值点,可令最小值为0,解方程可得m,λ,进而得到所求最小值.
,x>0,求出导数和单调区间、极小值点m和最小值点,可令最小值为0,解方程可得m,λ,进而得到所求最小值.
实数λ>0,若对任意的x∈(0,+∞),不等式eλx![]() 0恒成立,
0恒成立,
即为(eλx![]() )min≥0,
)min≥0,
设f(x)=eλx![]() ,x>0,f′(x)=λeλx
,x>0,f′(x)=λeλx![]() ,
,
令f′(x)=0,可得eλx![]() ,
,
由指数函数和反比例函数在第一象限的图象,
可得y=eλx和y![]() 有且只有一个交点,
有且只有一个交点,
设为(m,n),当x>m时,f′(x)>0,f(x)递增;
当0<x<m时,f′(x)<0,f(x)递减.
即有f(x)在x=m处取得极小值,且为最小值.
即有eλm![]() ,令eλm
,令eλm![]() 0,
0,
可得m=e,λ![]() .
.
则当λ![]() 时,不等式eλx
时,不等式eλx![]() 0恒成立.
0恒成立.
故答案为![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案【题目】某教育部门为了了解某地区高中学生每周的课外羽毛球训练的情况,随机抽取了该地区50名学生进行调查,其中男生25人.将每周课外训练时间不低于8小时的学生称为“训练迷”,低于8小时的学生称为“非训练迷”.已知“训练迷”中有15名男生.根据调查结果绘制的学生每周课外训练时间的频率分布直方图(时间单位为小时)如图所示.
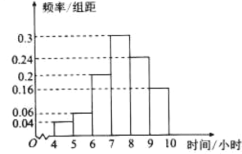
(1)根据图中数据估计该地区高中学生每周课外训练的平均时间(说明:同一组中的数据用该组区间的中间值作代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
非训练迷 | 训练迷 | 合计 | |
男 | |||
女 | |||
合计 |
(3)将每周课外训练时间为4-6小时的称为“业余球迷”,已知调查样本中,有3名“业余球迷”是男生,若从“业余球迷”中任意选取2人,求至少有1名男生的概率.
附: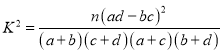 .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |