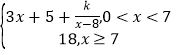题目内容
【题目】某种产品的质量以其质量指标值![]() 来衡量.当
来衡量.当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品;当
时,产品为二等品;当![]() 时,产品为三等品.现从甲、乙两条生产线,各随机抽取了100件该产品作为样本,测量每件产品的质量指标值,整理得到甲、乙两条生产线产品的质量指标值的频率分布直方图如图所示,视样本的频率为总体的概率.
时,产品为三等品.现从甲、乙两条生产线,各随机抽取了100件该产品作为样本,测量每件产品的质量指标值,整理得到甲、乙两条生产线产品的质量指标值的频率分布直方图如图所示,视样本的频率为总体的概率.


(1)若从甲、乙生产线生产的产品中各随机抽取1件,求恰好抽到1件一等品的概率;
(2)若一件三等品、二等品、一等品的利润分别为10元、20元、30元,从乙生产线生产的产品中随机抽取2件,求这两件产品的利润之和![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若从甲生产线生产的产品中随机抽取![]() 件,其中抽到二等品的件数为随机变量
件,其中抽到二等品的件数为随机变量![]() ,且
,且![]() 的数学期望不小于1200,求
的数学期望不小于1200,求![]() 的最小值.
的最小值.
【答案】(1)0.5;(2)分布列详见解析,数学期望为48;(3)3000.
【解析】
(1)根据频率分布直方图,分别求得甲、乙生产线为一等品的概率,再分一等品来自甲或乙两类求解.
(2)根据频率分布直方图,分别求得乙生产线为二等品,三等品的概率,根据一件三等品、二等品、一等品的利润分别为10元、20元、30元,得到两件产品的利润之和![]() 的取值有:20,30,40,50,60,分别求得其概率,列出分布列再求期望.
的取值有:20,30,40,50,60,分别求得其概率,列出分布列再求期望.
(3)根据从甲生产线抽到二等品的件数服从二项分布:![]() ,则由
,则由![]() 求解.
求解.
(1)由频率分布直方图可知,甲生产线为一等品的概率为![]() ,
,
乙生产线为一等品的概率为![]() ,
,
记![]() “恰抽到1件一等品”,
“恰抽到1件一等品”,
则![]() .
.
(2)由频率分布直方图可知,乙生产线为二等品的概率为![]() ,
,
乙生产线为三等品的概率为![]() ,
,
两件产品的利润之和![]() 的取值有:20,30,40,50,60,
的取值有:20,30,40,50,60,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 的分布列为
的分布列为
| 20 | 30 | 40 | 50 | 60 |
| 0.01 | 0.08 | 0.26 | 0.4 | 0.25 |
所以![]() .
.
(3)因为从甲生产线抽到二等品的件数![]() ,
,
所以![]() ,解得
,解得![]() ,所以
,所以![]() 的最小值为3000.
的最小值为3000.

 中考解读考点精练系列答案
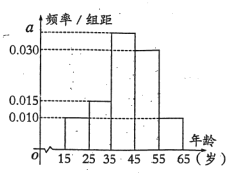
中考解读考点精练系列答案【题目】某教育部门为了了解某地区高中学生每周的课外羽毛球训练的情况,随机抽取了该地区50名学生进行调查,其中男生25人.将每周课外训练时间不低于8小时的学生称为“训练迷”,低于8小时的学生称为“非训练迷”.已知“训练迷”中有15名男生.根据调查结果绘制的学生每周课外训练时间的频率分布直方图(时间单位为小时)如图所示.
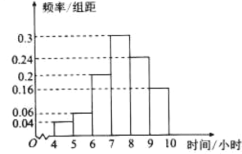
(1)根据图中数据估计该地区高中学生每周课外训练的平均时间(说明:同一组中的数据用该组区间的中间值作代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
非训练迷 | 训练迷 | 合计 | |
男 | |||
女 | |||
合计 |
(3)将每周课外训练时间为4-6小时的称为“业余球迷”,已知调查样本中,有3名“业余球迷”是男生,若从“业余球迷”中任意选取2人,求至少有1名男生的概率.
附: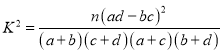 .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |