题目内容
12.若函数$f(x)=({1+\frac{1}{tanax}}){sin^2}ax-2sin({ax+\frac{π}{4}})sin({ax-\frac{π}{4}})$(a>0)的图象与直线y=m相切,相邻切点之间的距离为$\frac{π}{2}$.(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈[0,$\frac{π}{2}$],求点A的坐标.
分析 (1)运用切化弦,诱导公式和二倍角公式,两角和的正弦公式,化简整理f(x)的解析式,再有切线的意义和切点间的距离,可得周期,进而求得a,由正弦函数的值域,求得m;
(2)运用正弦函数的对称中心,解方程可得x,由x的范围求得k,进而得到点A的坐标.
解答 解:(1)$f(x)=({1+\frac{1}{tanax}}){sin^2}ax-2sin({ax+\frac{π}{4}})sin({ax-\frac{π}{4}})$
=${sin^2}ax+\frac{1}{tanax}•{sin^2}ax-2cos({\frac{π}{4}-ax})sin({ax-\frac{π}{4}})$
=${sin^2}ax+cosax•sinax+2cos({\frac{π}{4}-ax})sin({\frac{π}{4}-ax})$
=${sin^2}ax+cosaxsinax+sin({\frac{π}{2}-2ax})$
=sin2ax+cosaxsinax+cos2ax
=sin2ax+cosaxsinax+cos2ax-sin2ax
=${cos^2}ax+cosax•sinax=\frac{{\sqrt{2}}}{2}sin({2ax+\frac{π}{4}})+\frac{1}{2}$,
由题意知,m为f(x)的最大值或最小值,
所以$m=\frac{{1-\sqrt{2}}}{2}$或$m=\frac{{1+\sqrt{2}}}{2}$,
由题设知,函数f(x)的周期为$\frac{π}{2}$,
即$\frac{2π}{2a}$=$\frac{π}{2}$,解得a=2,
则$m=\frac{{1-\sqrt{2}}}{2}$或$m=\frac{{1+\sqrt{2}}}{2}$,a=2.
(2)∵f(x)=$\frac{{\sqrt{2}}}{2}sin({4x+\frac{π}{4}})+\frac{1}{2}$,
∴令$sin({4x+\frac{π}{4}})=0$,得$4x+\frac{π}{4}$=kπ(k∈Z),
∴$x=\frac{kπ}{4}-\frac{π}{16}$(k∈Z),
由0≤$\frac{kπ}{4}-\frac{π}{16}$≤$\frac{π}{2}$ (k∈Z),得k=1或k=2,
因此点A的坐标为$({\frac{3π}{16},\frac{1}{2}}),({\frac{7π}{16},\frac{1}{2}})$.
点评 本题考查三角函数的化简和求值,以及正弦函数的最值和周期,对称中心,同时考查切线的意义,属于中档题.

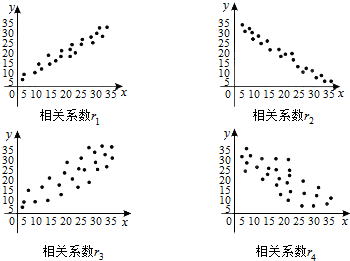
| A. | r2<r4<0<r3<r1 | B. | r4<r2<0<r1<r3 | C. | r4<r2<0<r3<r1 | D. | r2<r4<0<r1<r3 |
| A. | $[{-\frac{3}{2}-\sqrt{2},-\frac{3}{2}+\sqrt{2}}]$ | B. | $[{-\frac{3}{2}-\sqrt{2},\frac{5}{3}}]$ | C. | $[{\frac{3}{2}+\sqrt{2},\frac{5}{3}}]$ | D. | $[{-\frac{10}{3},-\frac{3}{2}-\sqrt{2}}]$ |
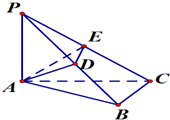 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PB中点,E为PC的中点,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PB中点,E为PC的中点,