题目内容
1．已知以点A（-1，2）为圆心的圆与直线m：x+2y+7=0相切，过点B（-2，0）的动直线l与圆A相交于M、N两点（1）求圆A的方程．
（2）当|MN|=2$\sqrt{19}$时，求直线l方程．
分析 （1）利用圆心到直线的距离公式求圆的半径，从而求解圆的方程；
（2）根据相交弦长公式，求出圆心到直线的距离，设出直线方程，再根据点到直线的距离公式确定直线方程．
解答 解：（1）意知A（-1，2）到直线x+2y+7=0的距离为圆A半径r，
∴$r=\frac{|-1+4+7|}{{\sqrt{5}}}=2\sqrt{5}$，
∴圆A方程为（x+1）2+（y-2）2=20（5分）
（2）垂径定理可知∠MQA=90°．且$MQ=\sqrt{19}$，
在Rt△AMQ中由勾股定理易知$AQ=\sqrt{A{M^2}-M{Q^2}}=1$
设动直线l方程为：y=k（x+2）或x=-2，显然x=-2合题意．
由A（-1，2）到l距离为1知$\frac{|-k+2k-2|}{{\sqrt{1+{k^2}}}}=1得k=\frac{3}{4}$．
∴3x-4y+6=0或x=-2为所求l方程．（7分）
点评 本题考查圆的标准方程及直线与圆的相交弦长问题，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
11．已知i为虚数单位，复数z=$\frac{i}{1+\sqrt{3}?i}$，则复数$\overline{z}$=（ ）
| A． | $\frac{\sqrt{3}}{4}$-$\frac{1}{4}$i | B． | $\frac{\sqrt{3}}{4}$+$\frac{1}{4}$i | C． | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$i | D． | $\frac{\sqrt{3}}{2}$-$\frac{1}{2}$i |
13．A={x|（a-2）x2-2（a-2）x-4＜0}，若A=R（R为实数集），则实数a的取值范围为（ ）
| A． | （-2，2） | B． | （-2，+∞） | C． | （-2，2] | D． | ∅ |
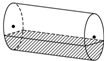一个水平放置的圆柱形储油桶（如图所示），桶内有油部分所在圆弧占底面圆周长的$\frac{1}{4}$，则油桶直立时，油的高度与桶的高度的比值是$\frac{1}{4}$-$\frac{1}{2π}$．（结果保留π）