题目内容
20.已知函数f(x)=ex-x-1(x≥0),g(x)=-x2+4x-3,若f(a)=g(b),则b的最大值是3.分析 由已知中函数的解析式可得f(x)≥f(0)=0,而g(x)≥0时,b∈[1,3],进而得到答案.
解答 解:∵函数f(x)=ex-x-1(x≥0),
∴f′(x)=ex-1(x≥0),
∵f′(x)≥0恒成立(x≥0),
∴f(x)≥f(0)=0,
即函数f(x)=ex-x-1(x≥0)的最小值为0,
又∵g(x)=-x2+4x-3的图象是开口朝下,且以直线x=2为对称轴,且与x轴交于(1,0),(3,0)点的抛物线,
若f(a)=g(b),
则b∈[1,3],
即b的最大值是3,
故答案为:3
点评 本题考查的知识点是函数的最值及其应用,指数函数的图象和性质,二次函数的图象和性质,是函数的图象和性质的简单综合应用,难度中档.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
10.已知向量$\overrightarrow{a}$=(x+z,3),$\overrightarrow{b}$=(2,y-z),且$\overrightarrow{a}$⊥$\overrightarrow{b}$.若x,y满足不等式$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤2}\end{array}\right.$,则z的取值范围为( )
| A. | [-6,4] | B. | [-4,6] | C. | [0,4] | D. | [0,6] |
11.已知i为虚数单位,复数z=$\frac{i}{1+\sqrt{3}?i}$,则复数$\overline{z}$=( )
| A. | $\frac{\sqrt{3}}{4}$-$\frac{1}{4}$i | B. | $\frac{\sqrt{3}}{4}$+$\frac{1}{4}$i | C. | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$i | D. | $\frac{\sqrt{3}}{2}$-$\frac{1}{2}$i |
5.在△ABC中,已知sinA=2sinB•cosC,且(a+b+c)(b+c-a)=3bc,则△ABC为( )
| A. | 等边三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
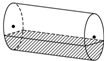 一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的$\frac{1}{4}$,则油桶直立时,油的高度与桶的高度的比值是$\frac{1}{4}$-$\frac{1}{2π}$.(结果保留π)
一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的$\frac{1}{4}$,则油桶直立时,油的高度与桶的高度的比值是$\frac{1}{4}$-$\frac{1}{2π}$.(结果保留π)