题目内容
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系: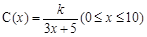 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
(1)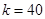 ,
,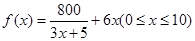 ;(2)隔热层修建5cm厚,总费用达到最小值70万元.
;(2)隔热层修建5cm厚,总费用达到最小值70万元.
解析试题分析:本题是实际应用题,考查了函数的最值(1)分别计算隔热层建造费用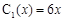 与20年的能源消耗费用之和
与20年的能源消耗费用之和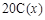 即可得
即可得 的表达式;(2)对函数
的表达式;(2)对函数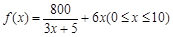 求导,研究函数的单调性,求得当
求导,研究函数的单调性,求得当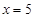 时
时 有最小值.在函数与导数知识的交汇处命题.
有最小值.在函数与导数知识的交汇处命题.
试题解析:(1)设隔热层厚度为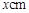 ,由题设,每年能源消耗费用为
,由题设,每年能源消耗费用为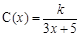
再由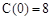 ,得
,得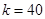 ,因此
,因此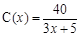 3分
3分
而建造费用为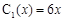 .
.
最后得隔热层建造费用与20年的能源消耗费用之和为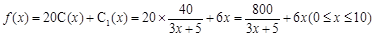 5分
5分
(2) .
.
解得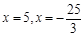 (舍去) 8分
(舍去) 8分
当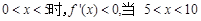 时,
时,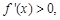 故
故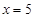 时,
时, 的最小值点,
的最小值点,
对应的最小值为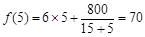 .
.
当隔热层修建5cm厚时,总费用达到最小值70万元. 12分
考点:1.待定系数求函数的解析式;2.函数的最值;3.导数法研究函数的单调性.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目

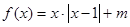
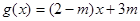 ,若方程
,若方程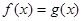 在
在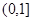 上有且仅一个实根,求实数
上有且仅一个实根,求实数 的取值范围;
的取值范围;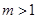 时,求函数
时,求函数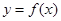 在
在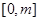 上的最大值.
上的最大值.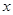 (元)与年产量
(元)与年产量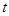 (吨)满足函数关系
(吨)满足函数关系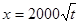 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场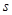 元(以下称
元(以下称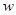 (元)表示为年产量
(元)表示为年产量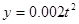 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格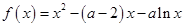 .
. 的单调区间
的单调区间 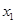 、
、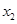 ,且
,且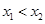 ,求证:
,求证: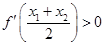 .
. 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为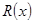 万元,且
万元,且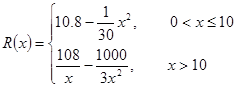 .
.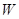 (万元)关于年产量
(万元)关于年产量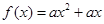 和
和 .其中
.其中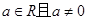 .
. 与
与 的图像的一个公共点恰好在
的图像的一个公共点恰好在 轴上,求
轴上,求 的值;
的值;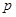 和
和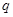 是方程
是方程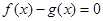 的两根,且满足
的两根,且满足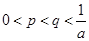 ,证明:当
,证明:当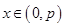 时,
时,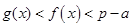 .
.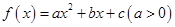 ,当
,当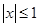 时,
时,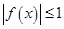 .
.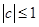 ;
;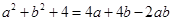 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 的表达式.
的表达式.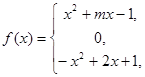
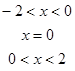 是奇函数.
是奇函数. 的值;
的值; 在区间
在区间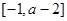 上单调递增,求实数
上单调递增,求实数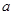 的取值范围;
的取值范围;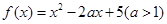 .
. 的定义域和值域均为
的定义域和值域均为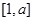 ,求实数
,求实数 的值;
的值; 上是减函数,且对任意的
上是减函数,且对任意的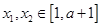 ,总有
,总有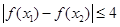 ,求实数
,求实数