题目内容
设函数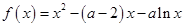 .
.
(1)求函数 的单调区间
的单调区间
(2)若函数 有两个零点
有两个零点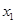 、
、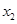 ,且
,且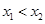 ,求证:
,求证: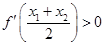 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)先求出函数 的定义域与导数
的定义域与导数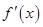 ,并对导数进行因式分解,然后对导数方程的根是否在定义域内进行分类讨论,从而确定函数
,并对导数进行因式分解,然后对导数方程的根是否在定义域内进行分类讨论,从而确定函数 相应的单调区间;(2)先利用函数
相应的单调区间;(2)先利用函数 有两个零点
有两个零点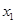 、
、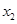 将
将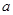 利用
利用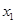 和
和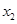 进行表示,于此同时,利用分析法将所要证明的问题进行转化,转化为
进行表示,于此同时,利用分析法将所要证明的问题进行转化,转化为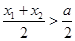 ,并结合前面
,并结合前面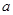 的结果,令
的结果,令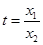 ,构造新函数利用导数来进行证明.
,构造新函数利用导数来进行证明.
试题解析:(1)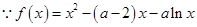 ,定义域为
,定义域为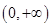 ,
, ,由于
,由于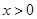 ,
, ,
,
①当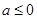 时,对任意
时,对任意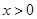 ,
, ,则函数
,则函数 的单调递增区间为
的单调递增区间为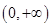 ;
;
②当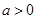 时,令
时,令 ,解得
,解得 ,
,
当 时,
时,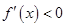 ,当
,当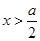 时,
时, ,
,
此时,函数 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
(2)因为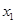 、
、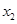 是函数
是函数 的两个零点,有
的两个零点,有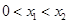 ,
,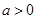
则 ,
, ,
,
两式相减得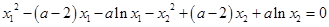 ,
,
即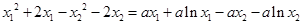

所以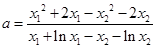
又因为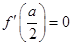 ,当
,当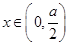 时,
时,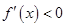 ;当
;当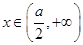 时,
时,
故只要证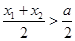 即可,即证明
即可,即证明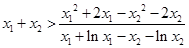 ,
,
即证明 ,
,
即证明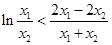 ,
,
设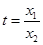
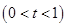 .令
.令 ,
,
则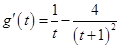
 ,因为
,因为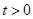 ,所以
,所以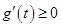 ,当且仅当
,当且仅当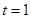 时,
时,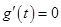
所以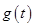 在
在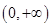 是增函数;又因为
是增函数;又因为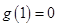 ,所以当
,所以当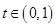 时,
时, 总成立.
总成立.
所以原题得证.
考点:1.分类讨论法;2.函数的单调区间;3.函数不等式

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目

 .
. ,集合
,集合 ,求
,求 ,
,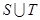 .
.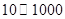 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
. ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 ; ②
; ②
 ,
, 时,解不等式
时,解不等式
 有最大值
有最大值 ,求实数
,求实数 的值.
的值.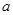 为实数,函数
为实数,函数 。
。 ,求
,求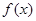 的最小值;
的最小值;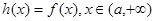 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式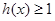 的解集.
的解集. 辟为水果园,其中
辟为水果园,其中 ,
, 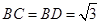 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 .
.
 的关系式;
的关系式; 的位置在哪里?
的位置在哪里?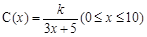 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和. .若
.若 的定义域为
的定义域为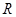 ,求实数
,求实数 的取值范围.
的取值范围.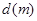 与车速
与车速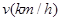 和车长
和车长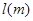 的关系满足:
的关系满足: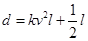 (
( 为正的常数),假定车身长为
为正的常数),假定车身长为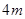 ,当车速为
,当车速为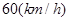 时,车距为2.66个车身长.
时,车距为2.66个车身长.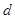 关于车速
关于车速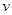 的函数关系式;
的函数关系式;