题目内容
已知函数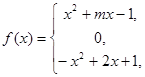
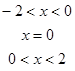 是奇函数.
是奇函数.
(1)求实数 的值;
的值;
(2)若函数 在区间
在区间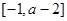 上单调递增,求实数
上单调递增,求实数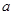 的取值范围;
的取值范围;
(3)求函数 的值域.
的值域.
(1)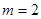 ;(2)
;(2) ;(3)
;(3)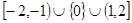 .
.
解析试题分析:(1)利用奇函数的定义,由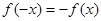 列式求解;(2)画出函数的图象,由图象列式
列式求解;(2)画出函数的图象,由图象列式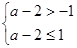 求解;(3)分段求值域:当
求解;(3)分段求值域:当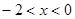 时,
时, =
= ;当
;当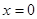 时,
时, =0;当
=0;当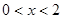 时,
时, =
=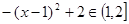 ,最后求并集得函数
,最后求并集得函数 的值域.
的值域.
试题解析:(1)当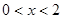 时,
时,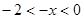 .∵
.∵ 是奇函数,∴
是奇函数,∴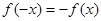 . 2分
. 2分
∴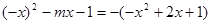 ,∴
,∴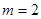 . 4分
. 4分
(2)由(1)得 =
= 由图象得
由图象得
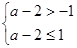 7分
7分
解得 . 8分
. 8分
(3)当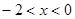 时,
时, =
= ;当
;当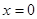 时,
时, =0;当
=0;当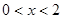 时,
时, =
=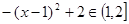 ,∴
,∴ 的值域为
的值域为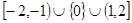 . 13分
. 13分
考点:函数的性质(单调性、奇偶性、值域).

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
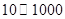 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
. ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 ; ②
; ②
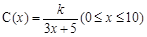 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和. .若
.若 的定义域为
的定义域为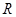 ,求实数
,求实数 的取值范围.
的取值范围. (升)关于行驶速度
(升)关于行驶速度 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.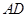 为半圆的直径,
为半圆的直径,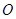 为半圆的圆心,
为半圆的圆心, ,
,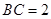 ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形 ,其底边
,其底边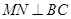 .
.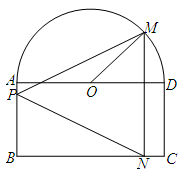
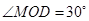 ,求三角形铁皮
,求三角形铁皮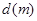 与车速
与车速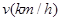 和车长
和车长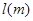 的关系满足:
的关系满足: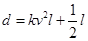 (
( 为正的常数),假定车身长为
为正的常数),假定车身长为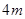 ,当车速为
,当车速为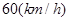 时,车距为2.66个车身长.
时,车距为2.66个车身长.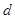 关于车速
关于车速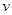 的函数关系式;
的函数关系式; 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.