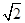题目内容
已知数列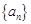 满足
满足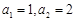 ,
,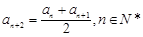 .
.
(1)令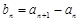 ,证明:
,证明: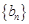 是等比数列;
是等比数列;
(2)求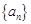 的通项公式.
的通项公式.
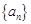 满足
满足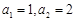 ,
,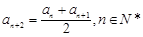 .
.(1)令
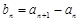 ,证明:
,证明: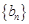 是等比数列;
是等比数列;(2)求
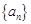 的通项公式.
的通项公式.(1)详见解析;(2)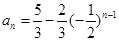 .
.
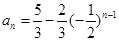 .
.试题分析:(1)要证明
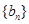 是等比数列,只需证明
是等比数列,只需证明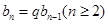 ,其中
,其中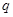 是不为零的常数,因此,只需把
是不为零的常数,因此,只需把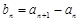 及
及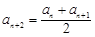 代入,即可得
代入,即可得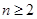 时,
时,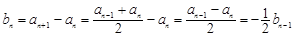 ,又由
,又由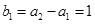 可得
可得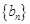 是首项为
是首项为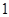 ,公比为
,公比为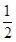 的等比数列,从而得证;(2)由(1)可得
的等比数列,从而得证;(2)由(1)可得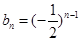 ,即有
,即有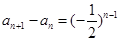 ,考虑采用累加法求其通项公式,即可得
,考虑采用累加法求其通项公式,即可得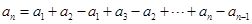
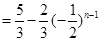 .
.(1)
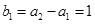 2分
2分当
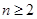 时,
时,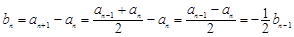 , 6分
, 6分∴
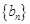 是首项为
是首项为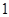 ,公比为
,公比为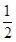 的等比数列; 8分
的等比数列; 8分(2)由(1)可得
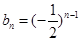 ,∴
,∴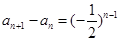 , 10分
, 10分∴
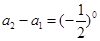 ,
,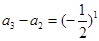 ,
,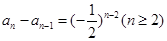 ,...............12分
,...............12分∴
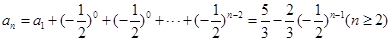 ,
,当
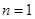 时,也符合,∴
时,也符合,∴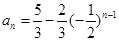 16分
16分 项和;2累加法求数列通项公式.
项和;2累加法求数列通项公式.
练习册系列答案
相关题目
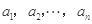 .对
.对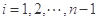 ,该数列前
,该数列前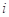 项的最大值记为
项的最大值记为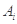 ,后
,后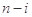 项
项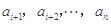 的最小值记为
的最小值记为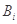 ,
,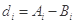 .
.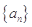 为3,4,7,1,写出
为3,4,7,1,写出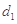 ,
,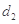 ,
,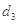 的值;
的值;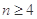 )是公比大于1的等比数列,且
)是公比大于1的等比数列,且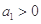 .证明:
.证明: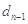 是等比数列.
是等比数列.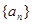 的前n项和为
的前n项和为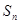 ,且
,且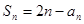 (
(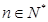 ).
).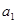 ,
,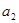 ,
,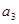 ,
,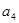 的值;
的值;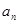 的表达式,并加以证明。
的表达式,并加以证明。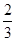 的等比数列
的等比数列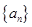 的前
的前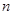 项和为
项和为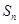 ,则 ( )
,则 ( )



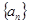 中,前n项和为
中,前n项和为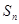 ,已知
,已知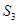 =8,
=8,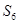 =7,则
=7,则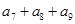 等于( )
等于( )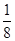


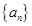 中,若
中,若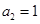 ,
,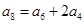 ,则
,则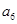 的值是 .
的值是 .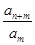 =an,则a3=________;{an}的前n项和Sn=________.
=an,则a3=________;{an}的前n项和Sn=________.