题目内容
设数列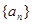 的前n项和为
的前n项和为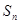 ,且
,且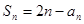 (
(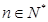 ).
).
(1)求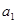 ,
,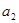 ,
,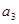 ,
,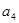 的值;
的值;
(2)猜想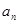 的表达式,并加以证明。
的表达式,并加以证明。
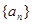 的前n项和为
的前n项和为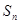 ,且
,且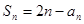 (
(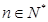 ).
).(1)求
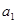 ,
,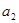 ,
,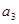 ,
,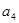 的值;
的值;(2)猜想
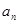 的表达式,并加以证明。
的表达式,并加以证明。(1) ,
, ,
, ,
, ; (2)猜想
; (2)猜想 (
(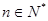 ),证明见解析.
),证明见解析.
 ,
, ,
, ,
, ; (2)猜想
; (2)猜想 (
(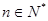 ),证明见解析.
),证明见解析.试题分析:(1)由条件
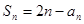 ,当
,当 时,有
时,有 ,解得
,解得 ,同理当
,同理当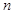 分别取2,3,4可得
分别取2,3,4可得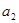 ,
,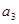 ,
,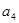 的值;(2)由(1)中前四项的值可猜想
的值;(2)由(1)中前四项的值可猜想 ,由
,由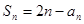 得
得 ,两式相减并化为
,两式相减并化为 ,则
,则 是等比数列,求出通项公式,可得
是等比数列,求出通项公式,可得 的通项公式.
的通项公式.解:(1)因为
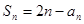 ,
, ,
,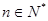 (1分)
(1分)所以,当
 时,有
时,有 ,解得
,解得 ; (2分)
; (2分)当
 时,有
时,有 ,解得
,解得 ; (3分)
; (3分)当
 时,有
时,有 ,解得
,解得 ; (4分)
; (4分)当
 时,有
时,有 ,解得
,解得 .(5分)
.(5分)(2)猜想
 (
(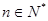 ) (9分)
) (9分)方法一:
由
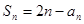 (
(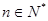 ),得
),得 (
( ), (10分)
), (10分)两式相减,得
 ,即
,即 (
( ).(11分)
).(11分)两边减2,得
 , (12分)
, (12分)所以{
 }是以-1为首项,
}是以-1为首项, 为公比的等比数列,
为公比的等比数列,故
 , (13分)
, (13分)即
 (
( ). (14分)
). (14分)方法二:
①当n=1时,由(1)可知猜想显然成立; (10分)
②假设当n=k时,猜想成立,即
 , (11分)
, (11分)由
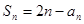 (
(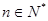 ),得
),得 ,
,
两式相减,得
 , (12分)
, (12分)所以
 ,
,即当n=k+1时,猜想也成立. (13分)
根据①和②,知对任意
 ,猜想成立.(14分)
,猜想成立.(14分)
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 ,
, .
. ;
; ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.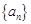 满足
满足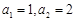 ,
,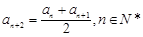 .
.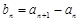 ,证明:
,证明: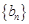 是等比数列;
是等比数列;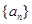 中,
中,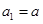 ,
, 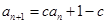 ,
, 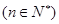
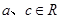 ,
,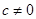
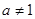 时,
时,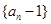 是等比数列,并求
是等比数列,并求


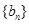 的前n项的和
的前n项的和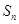 。
。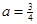 、
、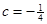 、
、 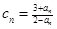 。记
。记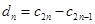 ,数列
,数列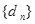 的前n项和
的前n项和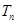 。证明:
。证明:
 中,
中, (c为非零常数)且前n项和
(c为非零常数)且前n项和 ,则实数k等于( ).
,则实数k等于( ). 1
1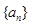 中,
中,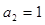 ,则其前
,则其前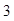 项的和
项的和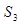 的取值范围是 ( )
的取值范围是 ( ) 



 (8n-1)
(8n-1)