题目内容
16．某企业生产甲乙两种产品均需用A，B两种原料，已知生产1吨每种产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为（ ）| 甲 | 乙 | 原料限额 | |
| A（吨） | 3 | 2 | 12 |
| B（吨） | 2 | 2 | 8 |
| A． | 12万元 | B． | 16万元 | C． | 17万元 | D． | 18万元 |
分析 设每天生产甲乙两种产品分别为x，y顿，利润为z元，然后根据题目条件建立约束条件，得到目标函数，画出约束条件所表示的区域，然后利用平移法求出z的最大值
解答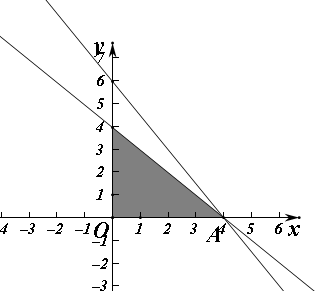 
解：设每天生产甲乙两种产品分别为x，y顿，利润为z元，
则$\left\{\begin{array}{l}{3x+2y≤12}\\{2x+2y≤8}\\{x≥0，y≥0}\end{array}\right.$，
目标函数为 z=3x+4y．
作出二元一次不等式组所表示的平面区域（阴影部分）即可行域
由z=3x+4y得y=-$\frac{3}{4}$x+$\frac{z}{4}$，
平移直线y=-$\frac{3}{4}$x+$\frac{z}{4}$，由图象可知当直线y=-$\frac{3}{4}$x+$\frac{z}{4}$经过点A时，直线y=-$\frac{3}{4}$x+$\frac{z}{4}$的截距最大，
此时z最大，
即经过点（0，4），
∴zmax=3x+4y=16．
即每天生产甲乙两种产品分别为0，4吨，能够产生最大的利润，最大的利润是16万元，
故选：B．
点评 本题主要考查线性规划的应用，建立约束条件和目标函数，利用数形结合是解决本题的关键
练习册系列答案
世纪百通期末金卷系列答案
相关题目
11．已知数列{an}满足：${a_1}=\frac{1}{7}$，对于任意的n∈N*，${a_{n+1}}=\frac{7}{2}{a_n}（1-{a_n}）$，则a999-a888=（ ）
| A． | $-\frac{2}{7}$ | B． | $\frac{2}{7}$ | C． | $-\frac{3}{7}$ | D． | $\frac{3}{7}$ |
8．若角α始边为x轴非负半轴，终边上一点A（1，-$\sqrt{3}$），则sinα等于（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
5．已知tanα=4$\sqrt{3}$，cos（α+β）=-$\frac{11}{14}$，α，β均为锐角，则β的值是（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |