题目内容
6.已知tanα=2,那么cos(2α+$\frac{3}{2}π}$)的值等于$\frac{4}{5}$.分析 利用二倍角的公式,诱导公式即可化简求值.
解答 解:∵tanα=2,
∴$cos(2α+\frac{3π}{2})$=cos(2α+π$+\frac{π}{2}$)=-cos(2α$+\frac{π}{2}$)=sin2α=$\frac{2sinαcosα}{{{{sin}^2}α+{{cos}^2}α}}$=$\frac{2tanα}{{{{tan}^2}α+1}}=\frac{4}{4+1}=\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题主要考查了二倍角的余弦函数公式,运用诱导公式化简求值,属于基础题.

练习册系列答案
相关题目
16.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
| 甲 | 乙 | 原料限额 | |
| A(吨) | 3 | 2 | 12 |
| B(吨) | 2 | 2 | 8 |
| A. | 12万元 | B. | 16万元 | C. | 17万元 | D. | 18万元 |
17.($\frac{-1+\sqrt{3}i}{2}$)2015=( )
| A. | $\frac{-1+\sqrt{3}i}{2}$ | B. | $\frac{-1-\sqrt{3}i}{2}$ | C. | -1 | D. | 1 |
14.设i为虚数单位,则复数$\frac{2i-1}{i}$=( )
| A. | 2+i | B. | 2-i | C. | -2-i | D. | -2+i |
11.如图,某几何体的三视图均为边长为1的正方形,则该几何体的表面积是( )
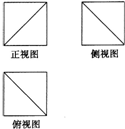

| A. | $\frac{{9+\sqrt{3}}}{2}$ | B. | $\frac{{12+\sqrt{3}}}{2}$ | C. | $\frac{{8+\sqrt{3}}}{2}$ | D. | $\frac{{9+2\sqrt{3}}}{2}$ |