题目内容
7.设集合M={-1,0,1},N={a,a2},则使N?M成立的a的值是-1.分析 由真子集的定义即知N的元素都是集合M的元素,从而分别让a取-1,0,1,看得到的集合N能否满足N?M,以及能否符合集合元素的性质,从而便得到a的值.
解答 解:N?M,∴N的元素都是M的元素;
若a=0,1时,显然不满足集合的互异性;
若a=-1,则N={-1,1},满足N?M;
∴a的值是-1.
故答案为:-1.
点评 考查列举法表示集合,真子集的定义,以及集合元素的性质.

练习册系列答案
相关题目
17.方程x2-4y2+3x-6y=0表示的图形是( )
| A. | 一条直线 | B. | 两条直线 | C. | 一个圆 | D. | 以上答案都不对 |
2.已知角α的终边上一点P(-3,4),则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
16.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
| 甲 | 乙 | 原料限额 | |
| A(吨) | 3 | 2 | 12 |
| B(吨) | 2 | 2 | 8 |
| A. | 12万元 | B. | 16万元 | C. | 17万元 | D. | 18万元 |
17.($\frac{-1+\sqrt{3}i}{2}$)2015=( )
| A. | $\frac{-1+\sqrt{3}i}{2}$ | B. | $\frac{-1-\sqrt{3}i}{2}$ | C. | -1 | D. | 1 |
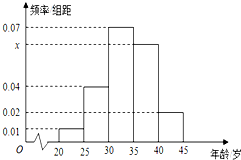 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].