题目内容
4.计算$\frac{\sqrt{2}sin(-1200°)}{tan\frac{7}{4}π}$-cos585°tan(-$\frac{37}{6}π$)分析 由条件利用诱导公式化简所给式子的值,可得结果.
解答 解:$\frac{\sqrt{2}sin(-1200°)}{tan\frac{7}{4}π}$-cos585°tan(-$\frac{37}{6}π$)=$\frac{\sqrt{2}•sin(-120°)}{tan(-\frac{π}{4})}$-cos225°•tan(-$\frac{π}{6}$)
=$\sqrt{2}$•$\frac{sin120°}{tan\frac{π}{4}}$+cos45°•(-tan$\frac{π}{6}$)=$\sqrt{2}$•$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}$•$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{6}}{3}$.
点评 本题主要考查利用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知a>0,b>0,则$6\sqrt{ab}+\frac{3}{a}+\frac{3}{b}$的最小值是( )
| A. | 10 | B. | $12\sqrt{2}$ | C. | 12 | D. | 20 |
16.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
| 甲 | 乙 | 原料限额 | |
| A(吨) | 3 | 2 | 12 |
| B(吨) | 2 | 2 | 8 |
| A. | 12万元 | B. | 16万元 | C. | 17万元 | D. | 18万元 |
14.设i为虚数单位,则复数$\frac{2i-1}{i}$=( )
| A. | 2+i | B. | 2-i | C. | -2-i | D. | -2+i |
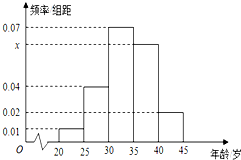 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].