题目内容
已知圆C:x2+y2=4,过点A(1,0)的直线与C相交于M 、N两点,则M 、N中点的轨迹方程为( )
A. | B. |
C. | D. |
A
设过A点斜率k存在时的直线方程为:y=k(x-1),代入x2+y2=4中有:
(1+k2)x2-2k2x+k2-4=0,设M,N的中点坐标为(x,y),则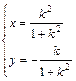 ,消去参数k,得
,消去参数k,得 ,
,
当斜率不存在时,M,N的中点为A点,此时也满足上式,故应选A。
(1+k2)x2-2k2x+k2-4=0,设M,N的中点坐标为(x,y),则
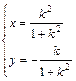 ,消去参数k,得
,消去参数k,得 ,
,当斜率不存在时,M,N的中点为A点,此时也满足上式,故应选A。

练习册系列答案
相关题目
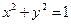 上的两动点,且满足与圆内一定点
上的两动点,且满足与圆内一定点 ,使
,使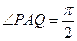 ,求过P和Q的两条切线的交点M的轨迹。
,求过P和Q的两条切线的交点M的轨迹。 ,则它的边与半径为
,则它的边与半径为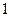 的圆的公共点个数最多为( )
的圆的公共点个数最多为( )



 的直线
的直线 与曲线
与曲线 有公共点,则直线
有公共点,则直线



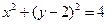 外一点
外一点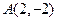 ,引圆的两条切线,切点为
,引圆的两条切线,切点为 ,则直线
,则直线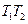 的方程为________。
的方程为________。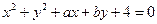 ,则直线
,则直线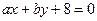
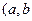 为非零常数)与圆M的位置关系是
为非零常数)与圆M的位置关系是  做圆的切线切于
做圆的切线切于 点,作割线交圆于
点,作割线交圆于 两点,其中
两点,其中
 ,则
,则 .
.