题目内容
设P,Q为圆周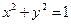 上的两动点,且满足与圆内一定点
上的两动点,且满足与圆内一定点 ,使
,使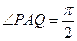 ,求过P和Q的两条切线的交点M的轨迹。
,求过P和Q的两条切线的交点M的轨迹。
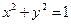 上的两动点,且满足与圆内一定点
上的两动点,且满足与圆内一定点 ,使
,使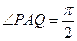 ,求过P和Q的两条切线的交点M的轨迹。
,求过P和Q的两条切线的交点M的轨迹。轨迹是以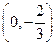 为圆心,
为圆心,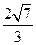 为半径的圆周
为半径的圆周
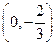 为圆心,
为圆心,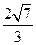 为半径的圆周
为半径的圆周解法一:连接PQ,OM,由圆的切线性质知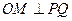 ,且PQ与OM交点E为PQ的中点。
,且PQ与OM交点E为PQ的中点。
…………5分
设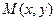 ,则
,则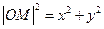 ,
,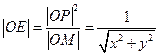 。从而得到E点的坐标为
。从而得到E点的坐标为
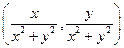 。 …………10分
。 …………10分
由于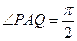 ,所以
,所以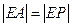 。又
。又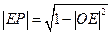 ,于是有
,于是有
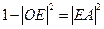 ,即有
,即有
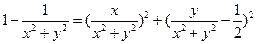 ………… 15分
………… 15分
化简得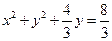 。
。
上述为以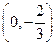 为圆心,
为圆心,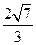 为半径的圆周。 …………20分
为半径的圆周。 …………20分
解法二:设P,Q的坐标为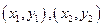 。由题意知,过P,Q的切线方程分别为
。由题意知,过P,Q的切线方程分别为
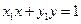 …………①,
…………①,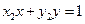 …………②
…………②
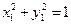 …………③
…………③
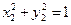 …………④ ………… 5分
…………④ ………… 5分
由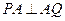 ,得
,得
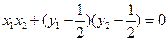 …………⑤
…………⑤
若①和②的交点仍记为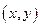 ,由此得到
,由此得到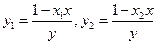 (
(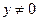 ) ………… 10分
) ………… 10分
代入③和④,得
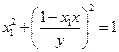
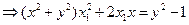
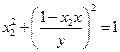
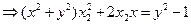
联立上述两式,即得
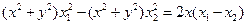 ………… 15分
………… 15分
因为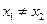 ,所以
,所以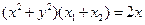 ,即
,即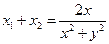 。
。
同理可得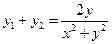 。于是有
。于是有
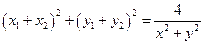
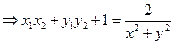
再由⑤式,推出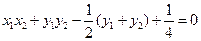 。
。
由上可得,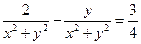 。
。
即有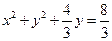 。
。
上述为以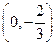 为圆心,
为圆心,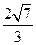 为半径的圆周。 …………20分
为半径的圆周。 …………20分
当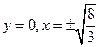 时,也符合题设所求的轨迹。
时,也符合题设所求的轨迹。
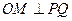 ,且PQ与OM交点E为PQ的中点。
,且PQ与OM交点E为PQ的中点。…………5分
设
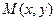 ,则
,则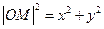 ,
,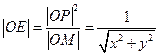 。从而得到E点的坐标为
。从而得到E点的坐标为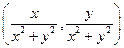 。 …………10分
。 …………10分由于
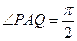 ,所以
,所以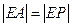 。又
。又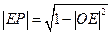 ,于是有
,于是有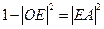 ,即有
,即有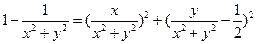 ………… 15分
………… 15分化简得
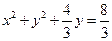 。
。上述为以
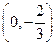 为圆心,
为圆心,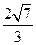 为半径的圆周。 …………20分
为半径的圆周。 …………20分解法二:设P,Q的坐标为
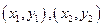 。由题意知,过P,Q的切线方程分别为
。由题意知,过P,Q的切线方程分别为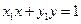 …………①,
…………①,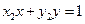 …………②
…………②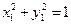 …………③
…………③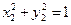 …………④ ………… 5分
…………④ ………… 5分由
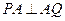 ,得
,得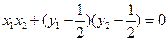 …………⑤
…………⑤若①和②的交点仍记为
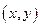 ,由此得到
,由此得到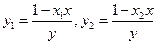 (
(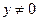 ) ………… 10分
) ………… 10分代入③和④,得
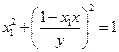
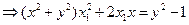
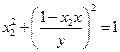
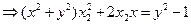
联立上述两式,即得
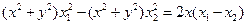 ………… 15分
………… 15分因为
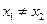 ,所以
,所以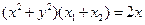 ,即
,即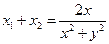 。
。同理可得
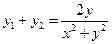 。于是有
。于是有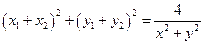
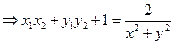
再由⑤式,推出
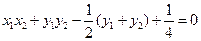 。
。由上可得,
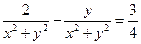 。
。即有
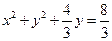 。
。上述为以
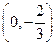 为圆心,
为圆心,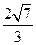 为半径的圆周。 …………20分
为半径的圆周。 …………20分当
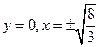 时,也符合题设所求的轨迹。
时,也符合题设所求的轨迹。
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 满足
满足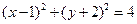 ,求
,求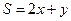 的最大值和最小值.
的最大值和最小值.



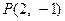 为圆
为圆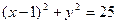 的弦
的弦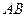 的中点,则直线
的中点,则直线
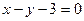 B
B
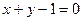 D
D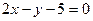
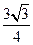 B.
B.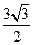 C.
C.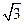 D.3
D.3