题目内容
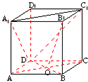
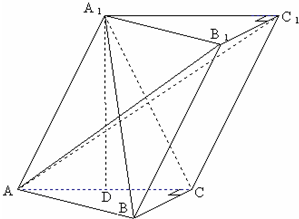
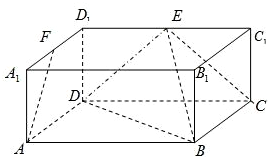
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E、F分别为C1D1、A1D1的中点.
(Ⅰ)求证:DE⊥平面BCE;
(Ⅱ)求证:AF∥平面BDE.
(Ⅰ)求证:DE⊥平面BCE;
(Ⅱ)求证:AF∥平面BDE.

(Ⅰ)证明:∵BC⊥侧面CDD1C1,DE?侧面CDD1C1,
∴DE⊥BC,(3分)
在△CDE中,CD=2a,CE=DE=
a,则有CD2=CE2+DE2,
∴∠DEC=90°,
∴DE⊥EC,(6分)
又BC∩EC=C
∴DE⊥平面BCE.(7分)
(Ⅱ)证明:连EF、A1C1,连AC交BD于O,
∵EF
A1C1,AO
A1C1,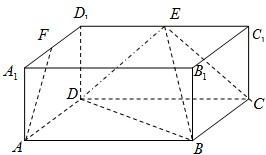
∴四边形AOEF是平行四边形,(10分)
∴AF∥OE(11分)
又∵OE?平面BDE,AF?平面BDE,
∴AF∥平面BDE.(14分)
∴DE⊥BC,(3分)
在△CDE中,CD=2a,CE=DE=
| 2 |
∴∠DEC=90°,
∴DE⊥EC,(6分)
又BC∩EC=C
∴DE⊥平面BCE.(7分)
(Ⅱ)证明:连EF、A1C1,连AC交BD于O,
∵EF
| ||
| . |
| 1 |
| 2 |
| ||
| . |
| 1 |
| 2 |

∴四边形AOEF是平行四边形,(10分)
∴AF∥OE(11分)
又∵OE?平面BDE,AF?平面BDE,
∴AF∥平面BDE.(14分)

练习册系列答案
相关题目