题目内容
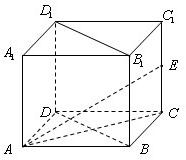
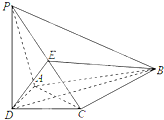
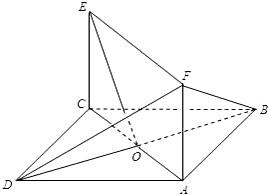
在直角梯形ABCD中,∠ABC=∠BAD=90°,BE⊥平面ABCD,AB=BC=BE=2AD=2.
(Ⅰ)求异面直线DE与AC所成角的大小;
(Ⅱ)在线段CE上是否存在点F,使平面BDF⊥平面ADE,若存在,确定点F的位置,若不存在,请说明理由.
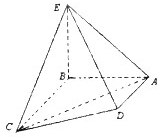
(Ⅰ)求异面直线DE与AC所成角的大小;
(Ⅱ)在线段CE上是否存在点F,使平面BDF⊥平面ADE,若存在,确定点F的位置,若不存在,请说明理由.

由于在直角梯形ABCD中,∠ABC=∠BAD=90°,BE⊥平面ABCD,
则AB,BC,BE两两垂直,
故可以B为原点建立如图所示空间直角坐标系B-xyz.
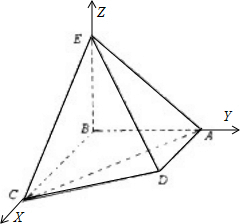
∵AB=BC=BE=2AD=2,
则B(0,0,0),A(0,2,0),C(2,0,0),D(1,2,0),E(0,0,2).
(Ⅰ)∵
=(-1,-2,2),
=(2,-2,0)
∴
•
=(-1)×2+(-2)×(-2)=2,
|
|=
=3,
|
|=
=2
∴cos<
,
>=
=
故异面直线DE与AC所成角的大小为arccos
;
(Ⅱ)假设线段CE上存在这样的点F,不妨设F(a,0,2-a)(0≤a≤2)
则
=(1,2,0),
=(a,0,2-a)
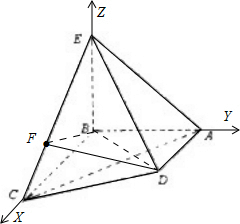
若设平面BDF的法向量为
=(x,y,z)
故有
,则
∴平面BDF的一个法向量为
=(2,-1,-
)
∵在平面ADE中,
=(-1,-2,2),
=(1,0,0)
同理可得平面ADE的一个法向量为
=(0,1,1)
由于平面BDF⊥平面ADE,则
⊥
,
即
•
=2×0+(-1)×1+(-
)×1=0
解得a=-2,由于点F在线段CE上,-2∉{a|0≤a≤2}
故在线段CE上不存在点F,使得平面BDF⊥平面ADE.
则AB,BC,BE两两垂直,
故可以B为原点建立如图所示空间直角坐标系B-xyz.

∵AB=BC=BE=2AD=2,
则B(0,0,0),A(0,2,0),C(2,0,0),D(1,2,0),E(0,0,2).
(Ⅰ)∵
| DE |
| AC |
∴
| DE |
| AC |
|
| DE |
| (-1)2+(-2)2+22 |
|
| AC |
| 22+(-2)2+02 |
| 2 |
∴cos<
| DE |
| AC |
| ||||
|
|
| ||
| 6 |
故异面直线DE与AC所成角的大小为arccos
| ||
| 6 |
(Ⅱ)假设线段CE上存在这样的点F,不妨设F(a,0,2-a)(0≤a≤2)
则
| BD |
| BF |

若设平面BDF的法向量为
| n |
故有
|
|
∴平面BDF的一个法向量为
| n |
| 2a |
| 2-a |
∵在平面ADE中,
| DE |
| AD |
同理可得平面ADE的一个法向量为
| m |
由于平面BDF⊥平面ADE,则
| m |
| n |
即
| m |
| n |
| 2a |
| 2-a |
解得a=-2,由于点F在线段CE上,-2∉{a|0≤a≤2}
故在线段CE上不存在点F,使得平面BDF⊥平面ADE.

练习册系列答案
相关题目