题目内容
已知四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为2的正方形,SA=2,AC与BD相交于点O.
(1)证明:SO⊥BD;
(2)求三棱锥O-SCD的体积.
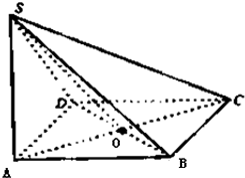
(1)证明:SO⊥BD;
(2)求三棱锥O-SCD的体积.

(1)证明:∵底面ABCD是正方形,∴AC⊥BD,
又侧棱SA⊥底面ABCD,∴SA⊥BD,AC∩SA=A,
∴BD⊥平面SAC,SO?平面SAC,∴SO⊥BD;
(2)∵底面正方形的边长为2,∴S△OCD=
×2×2=1,
∵SA⊥底面ABCD,∴SA为三棱锥O-SCD的高,SA=2.
∴VO-SCD=VS-OCD=
×1×2=
.
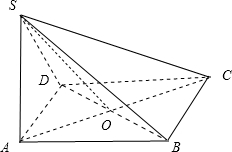
又侧棱SA⊥底面ABCD,∴SA⊥BD,AC∩SA=A,
∴BD⊥平面SAC,SO?平面SAC,∴SO⊥BD;
(2)∵底面正方形的边长为2,∴S△OCD=
| 1 |
| 4 |
∵SA⊥底面ABCD,∴SA为三棱锥O-SCD的高,SA=2.
∴VO-SCD=VS-OCD=
| 1 |
| 3 |
| 2 |
| 3 |


练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目