题目内容
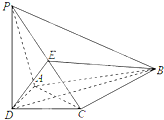
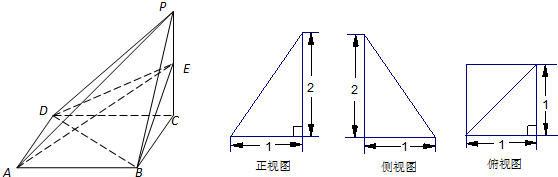
已知一个四棱锥P-ABCD的三视图（正视图与侧视图为直角三角形，俯视图是带有一条对角形的正方形）如下，E是侧棱PC上的动点．
（1）求四棱锥P-ABCD的体积；
（2）是否不论点E在何位置都有BD⊥AE，证明你的结论．
（1）求四棱锥P-ABCD的体积；
（2）是否不论点E在何位置都有BD⊥AE，证明你的结论．
（1）由三视图可知，PC⊥面ABCD，且PC=2，
底面ABCD是正方形，故体积Vp-ABCD=
×2×1×1=
；（6分）
（2）是，在任何位置都有BD⊥AE，理由如下：（8分）
连接AC，则AC⊥BD，PC⊥BD且PC交AC于C点，故BD⊥面PAC，
因为E是PC上的动点，所以AE在平面PAC内，所以BD⊥AE不论E在何位置都正确．（12分）
底面ABCD是正方形，故体积Vp-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |
（2）是，在任何位置都有BD⊥AE，理由如下：（8分）
连接AC，则AC⊥BD，PC⊥BD且PC交AC于C点，故BD⊥面PAC，
因为E是PC上的动点，所以AE在平面PAC内，所以BD⊥AE不论E在何位置都正确．（12分）
练习册系列答案
相关题目
