题目内容
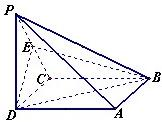
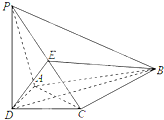
如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)设M在线段AB上,且满足AM=3MB,线段CE上是否存在一点N,使得MN∥平面DAE?若存在,求出CN的长;若不存在,说明理由.
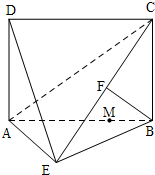
(1)求证:AE⊥BE;
(2)设M在线段AB上,且满足AM=3MB,线段CE上是否存在一点N,使得MN∥平面DAE?若存在,求出CN的长;若不存在,说明理由.

(1)证明:∵AD⊥平面ABE,AD∥BC
∴BC⊥平面ABE,∴AE⊥BC
又∵BF⊥平面ACE,∴AE⊥BF
∵BC∩BF=B,
∴AE⊥平面BCE,
∵BE?平面BCE,∴AE⊥BE;
(2)存在CN=
CE,使得MN∥平面DAE.
在△ABE中过M点作MG∥AE交BE于G点,在△BEC中过G点作GN∥BC交EC于N点,连MN,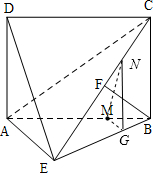
∵AM=3MB,∴CN=
CE
∵MG∥AE,MG?平面ADE,AE?平面ADE,∴MG∥平面ADE
同理可证,GN∥平面ADE,
∵MG∩GN=G,∴平面MGN∥平面ADE
又∵MN?平面MGN,∴MN∥平面ADE,
∵EB=BC=2,∴CE=2
∴CN=
∴BC⊥平面ABE,∴AE⊥BC
又∵BF⊥平面ACE,∴AE⊥BF
∵BC∩BF=B,
∴AE⊥平面BCE,
∵BE?平面BCE,∴AE⊥BE;
(2)存在CN=
| 1 |
| 4 |
在△ABE中过M点作MG∥AE交BE于G点,在△BEC中过G点作GN∥BC交EC于N点,连MN,

∵AM=3MB,∴CN=
| 1 |
| 4 |
∵MG∥AE,MG?平面ADE,AE?平面ADE,∴MG∥平面ADE
同理可证,GN∥平面ADE,
∵MG∩GN=G,∴平面MGN∥平面ADE
又∵MN?平面MGN,∴MN∥平面ADE,
∵EB=BC=2,∴CE=2
| 2 |
∴CN=
| ||
| 2 |

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目