Question

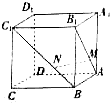
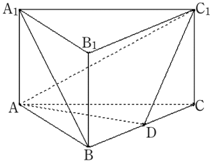
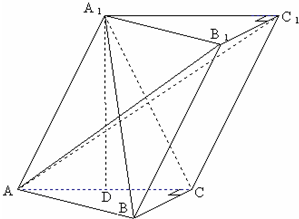
如图，已知斜三棱柱ABC-A₁B₁C₁，∠BCA=90°，AC=BC=2，A₁在底面ABC上的射影恰为AC的中点D，且BA₁⊥AC₁．
（1）求证：AC₁⊥平面A₁BC；
（2）求多面体B₁C₁ABC的体积．

Answer 1

（1）证明：

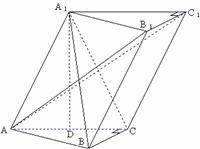
A₁在底面ABC上的射影在AC上⇒A₁D⊥平面ABC⇒A₁D⊥BC，∵AC⊥BC，
∴BC⊥平面A₁C₁CA…（3分）AC₁?平面A₁C₁CA，∴BC⊥AC₁，BA₁⊥AC₁，A₁B∩BC=B，∴AC₁⊥平面A₁BC…（7分）
（2）由（1）可知：A₁C⊥AC₁⇒ACC₁A₁是棱形；…（9分）
∵AC=2，点D为中点，AD⊥BC，∴△A₁AC为正三角形，∴AD=

3

…（11分）
∴V多面体B1C1ABC=VA1B1C1-ABC-VA-A1B1C1=

2

3

VA1B1C1-ABC=

2

3

×

1

2

×4×

3

=

4 3

3

…（13分）