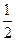题目内容
(本小题满分12分)设数列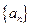 和
和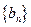 满足:
满足: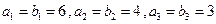 ,数列
,数列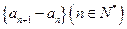 是等差数列,
是等差数列,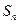 为数列
为数列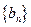 的前
的前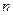 项和,且
项和,且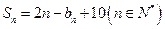 ,
,
(I)求数列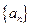 和
和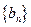 的通项公式;
的通项公式;
(II)是否存在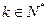 ,使
,使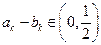 ?若存在,求出
?若存在,求出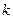 ,若不存在,说明理由。
,若不存在,说明理由。
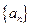 和
和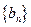 满足:
满足: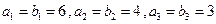 ,数列
,数列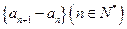 是等差数列,
是等差数列,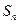 为数列
为数列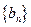 的前
的前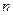 项和,且
项和,且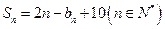 ,
,(I)求数列
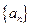 和
和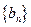 的通项公式;
的通项公式;(II)是否存在
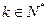 ,使
,使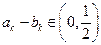 ?若存在,求出
?若存在,求出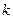 ,若不存在,说明理由。
,若不存在,说明理由。(I) ,
,
(II)不存在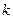 ,使
,使
 ,
,
(II)不存在
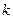 ,使
,使
(I)由已知





当 时,也满足上式,
时,也满足上式,

由

 ,即
,即 ,则
,则 ,
,
∴数列 是等比数列,公比
是等比数列,公比 ,
,


(II)设
当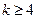 时:
时: 是
是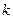 的增函数;
的增函数; 也是
也是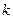 的增函数。
的增函数。
 时:
时: ,又
,又
 不存在
不存在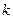 ,使
,使







当
 时,也满足上式,
时,也满足上式,

由


 ,即
,即 ,则
,则 ,
,∴数列
 是等比数列,公比
是等比数列,公比 ,
,

(II)设

当
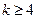 时:
时: 是
是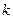 的增函数;
的增函数; 也是
也是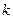 的增函数。
的增函数。
 时:
时: ,又
,又
 不存在
不存在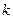 ,使
,使


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
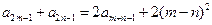
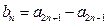 (n∈N*),证明:数列{bn}是等差数列;
(n∈N*),证明:数列{bn}是等差数列;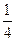
 qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.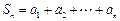 ,且
,且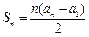 .
.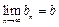 ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令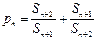 ,求数列
,求数列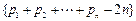 的“上渐近值”.
的“上渐近值”.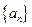 的前
的前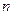 项和为
项和为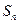 ,已知
,已知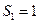 ,
,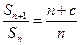 (
(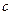 为常数,
为常数,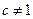 ,
,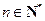 ),且
),且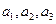 成等差数列.
成等差数列.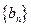 是首项为1,公比为
是首项为1,公比为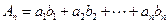 ,
,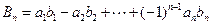 ,
,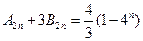 .
.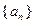 的公差是
的公差是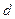 ,
,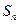 是该数列的前
是该数列的前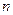 项和.
项和.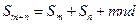 ;
;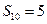 、
、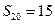 ,求
,求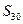 ”;
”;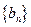 的公比为
的公比为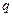 ,前
,前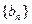 ,其中
,其中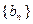 的前
的前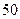 项和
项和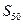 .”
.”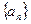 的通项公式为
的通项公式为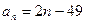 ,
,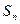 达到最小时,
达到最小时,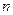 =______________.
=______________. 满足
满足 ,其中
,其中 为
为 项和,
项和, ;
; 是等比数列;
是等比数列; 和
和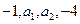 成等差数列,
成等差数列,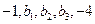 成等比数列,则
成等比数列,则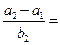 ( )
( )