题目内容
(本小题满分14分)
设数列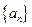 的前
的前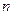 项和为
项和为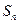 ,已知
,已知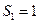 ,
,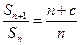 (
(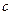 为常数,
为常数,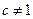 ,
,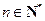 ),且
),且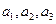 成等差数列.
成等差数列.
(1)求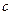 的值;
的值;
(2)求数列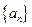 的通项公式;
的通项公式;
(3)若数列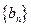 是首项为1,公比为
是首项为1,公比为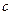 的等比数列,记
的等比数列,记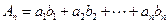 ,
,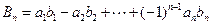 ,
,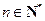 .证明:
.证明: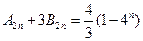 .
.
设数列
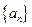 的前
的前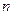 项和为
项和为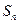 ,已知
,已知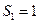 ,
,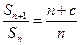 (
(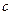 为常数,
为常数,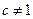 ,
,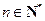 ),且
),且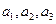 成等差数列.
成等差数列.(1)求
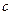 的值;
的值;(2)求数列
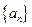 的通项公式;
的通项公式;(3)若数列
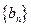 是首项为1,公比为
是首项为1,公比为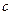 的等比数列,记
的等比数列,记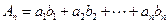 ,
,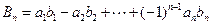 ,
,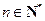 .证明:
.证明: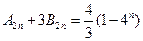 .
.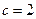 ,
,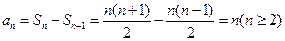
解:(新编题)
(1)∵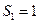 ,
,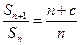 ,∴
,∴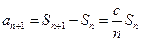 ,-------------------------2分
,-------------------------2分
∴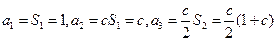 .
.
∵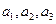 成等差数列,∴
成等差数列,∴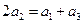 ,
,
即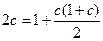 ,∴
,∴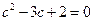 .---------------------------------------------------5分
.---------------------------------------------------5分
解得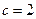 ,或
,或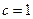 (舍去).-----------------------------------------------------------------6分
(舍去).-----------------------------------------------------------------6分
(2)∵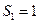 ,
,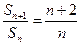 ,
,
∴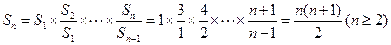 ,-------------------8分
,-------------------8分
∴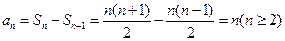 ,------------------------------------------9分
,------------------------------------------9分
又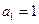 ,∴数列
,∴数列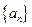 的通项公式是
的通项公式是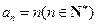 .-----------------------------------10分
.-----------------------------------10分
(3)证明:∵数列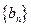 是首项为1,公比为
是首项为1,公比为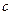 的等比数列,∴
的等比数列,∴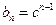 .---------11分
.---------11分
∵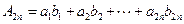 ,
,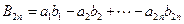 ,
,
∴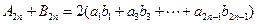 , ①
, ①
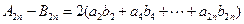 , ②
, ②
①式两边乘以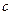 得
得 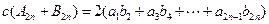 ③
③
由②③得
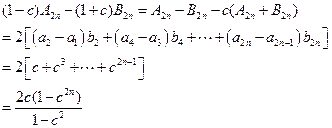
将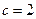 代入上式,得
代入上式,得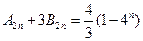 .-----------------------------------------14分
.-----------------------------------------14分
另证: 先用错位相减法求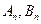 ,再验证
,再验证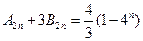 .
.
∵数列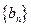 是首项为1,公比为
是首项为1,公比为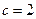 的等比数列,∴
的等比数列,∴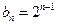 . --------------11分
. --------------11分
又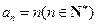 ,所以
,所以
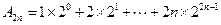 ①
①
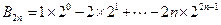 ②
②
将①乘以2得: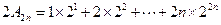 ③
③
①-③得: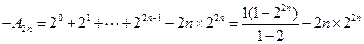 ,
,
整理得: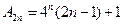 -------------------------12分
-------------------------12分
将②乘以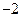 得:
得: 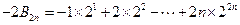 ④
④
②-④整理得:
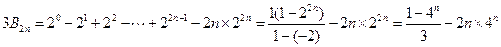
-----------------------------------------13分
∴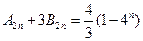 -----------------------------------------14分
-----------------------------------------14分
(1)∵
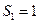 ,
,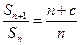 ,∴
,∴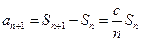 ,-------------------------2分
,-------------------------2分∴
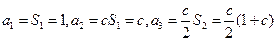 .
.∵
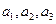 成等差数列,∴
成等差数列,∴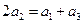 ,
,即
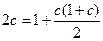 ,∴
,∴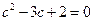 .---------------------------------------------------5分
.---------------------------------------------------5分解得
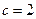 ,或
,或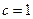 (舍去).-----------------------------------------------------------------6分
(舍去).-----------------------------------------------------------------6分(2)∵
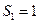 ,
,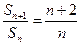 ,
,∴
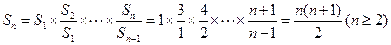 ,-------------------8分
,-------------------8分∴
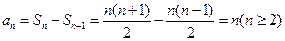 ,------------------------------------------9分
,------------------------------------------9分又
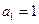 ,∴数列
,∴数列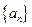 的通项公式是
的通项公式是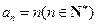 .-----------------------------------10分
.-----------------------------------10分(3)证明:∵数列
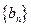 是首项为1,公比为
是首项为1,公比为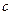 的等比数列,∴
的等比数列,∴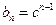 .---------11分
.---------11分∵
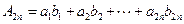 ,
,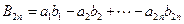 ,
,∴
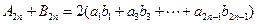 , ①
, ①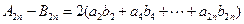 , ②
, ②①式两边乘以
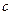 得
得 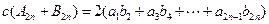 ③
③由②③得
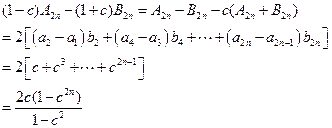
将
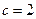 代入上式,得
代入上式,得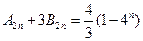 .-----------------------------------------14分
.-----------------------------------------14分另证: 先用错位相减法求
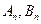 ,再验证
,再验证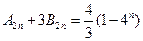 .
.∵数列
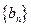 是首项为1,公比为
是首项为1,公比为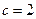 的等比数列,∴
的等比数列,∴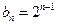 . --------------11分
. --------------11分又
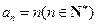 ,所以
,所以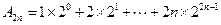 ①
①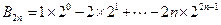 ②
②将①乘以2得:
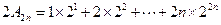 ③
③①-③得:
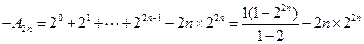 ,
,整理得:
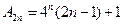 -------------------------12分
-------------------------12分将②乘以
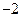 得:
得: 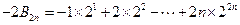 ④
④②-④整理得:
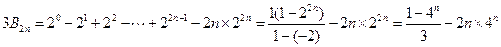
-----------------------------------------13分
∴
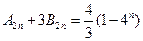 -----------------------------------------14分
-----------------------------------------14分
练习册系列答案
相关题目
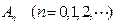 ,其中
,其中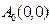 ,
,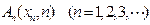 ,并且线段
,并且线段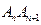 所在直线的斜率为
所在直线的斜率为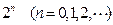 .
.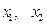
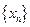 的通项公式
的通项公式
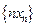 的前
的前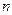 项和为
项和为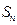 ,求
,求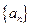 和
和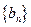 满足:
满足: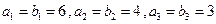 ,数列
,数列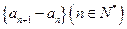 是等差数列,
是等差数列,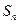 为数列
为数列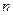 项和,且
项和,且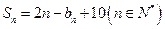 ,
,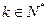 ,使
,使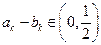 ?若存在,求出
?若存在,求出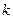 ,若不存在,说明理由。
,若不存在,说明理由。
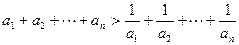 成立的最小自然数n是( )
成立的最小自然数n是( ) 中,
中, ,则它的前10项和为( )
,则它的前10项和为( )

 .
.




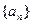 满足
满足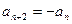 ,且
,且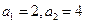 ,则该数列的前509项的和为 .
,则该数列的前509项的和为 .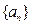 的各项均为正数,
的各项均为正数,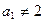 ,且前
,且前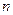 项之和
项之和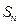 满足
满足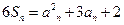 ,求数列的通项公式.
,求数列的通项公式.