题目内容
已知椭圆ε: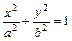 (a>b>0),动圆
(a>b>0),动圆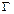 :
: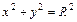 ,其中b<R<a. 若A是椭圆ε上的点,B是动圆
,其中b<R<a. 若A是椭圆ε上的点,B是动圆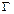 上的点,且使直线AB与椭圆ε和动圆
上的点,且使直线AB与椭圆ε和动圆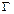 均相切,求A、B两点的距离
均相切,求A、B两点的距离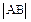 的最大值.
的最大值.
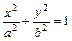 (a>b>0),动圆
(a>b>0),动圆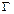 :
: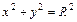 ,其中b<R<a. 若A是椭圆ε上的点,B是动圆
,其中b<R<a. 若A是椭圆ε上的点,B是动圆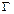 上的点,且使直线AB与椭圆ε和动圆
上的点,且使直线AB与椭圆ε和动圆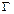 均相切,求A、B两点的距离
均相切,求A、B两点的距离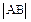 的最大值.
的最大值.
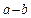
设A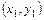 、B
、B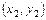 ,直线AB的方程为
,直线AB的方程为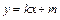 因为A既在椭圆
因为A既在椭圆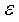 上又在直线AB上,从而有
上又在直线AB上,从而有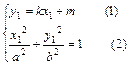 将(1)代入(2)得
将(1)代入(2)得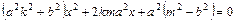
由于直线AB与椭圆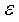 相切,故
相切,故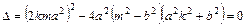
从而可得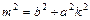 ,
,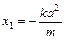 (3)……………………5分
(3)……………………5分
同理,由B既在圆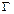 上又在直线AB上,可得
上又在直线AB上,可得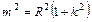 ,
,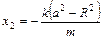 (4)………10分
(4)………10分
由(3)、(4)得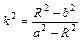 ,
,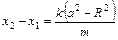
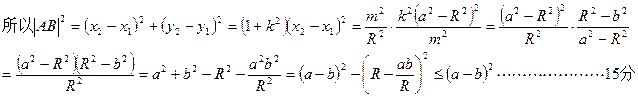 即
即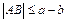 ,当且仅当
,当且仅当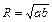 时取等号所以A、B两点的距离
时取等号所以A、B两点的距离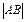 的最大值为
的最大值为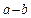 . ……………20分.
. ……………20分.
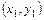 、B
、B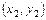 ,直线AB的方程为
,直线AB的方程为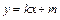 因为A既在椭圆
因为A既在椭圆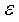 上又在直线AB上,从而有
上又在直线AB上,从而有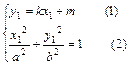 将(1)代入(2)得
将(1)代入(2)得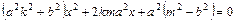
由于直线AB与椭圆
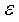 相切,故
相切,故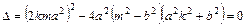
从而可得
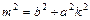 ,
,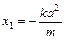 (3)……………………5分
(3)……………………5分同理,由B既在圆
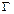 上又在直线AB上,可得
上又在直线AB上,可得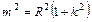 ,
,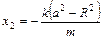 (4)………10分
(4)………10分由(3)、(4)得
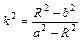 ,
,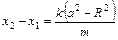
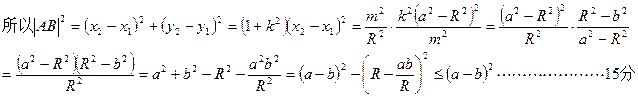 即
即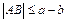 ,当且仅当
,当且仅当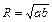 时取等号所以A、B两点的距离
时取等号所以A、B两点的距离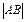 的最大值为
的最大值为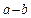 . ……………20分.
. ……………20分.
练习册系列答案
相关题目
 =1上一点,以点P以及焦点F1、F2为顶点的三角形的面积等于1,则P点的坐标为___________.
=1上一点,以点P以及焦点F1、F2为顶点的三角形的面积等于1,则P点的坐标为___________. 与曲线C恒有公共点,求
与曲线C恒有公共点,求 的取值范围.
的取值范围.
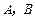 两点相距2千米,现准备在荒漠上围垦出一片以
两点相距2千米,现准备在荒漠上围垦出一片以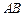 为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.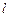 刚好通过点
刚好通过点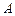 ,且
,且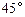 角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?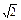 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆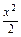 +y2=1有两个不同的交点P和Q.
+y2=1有两个不同的交点P和Q.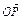 +
+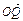 与
与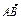 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.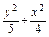 =1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
=1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.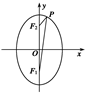
 ,-
,-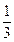 )
) ,
, ,
,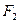 分别为其左、右焦点,
分别为其左、右焦点,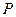 为椭圆上任意一点,
为椭圆上任意一点,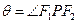 ,求
,求 的最大值及
的最大值及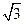 ,4+2
,4+2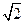 ,4+2
,4+2