题目内容
15.(1)已知a>1,求证:$\sqrt{a+1}$+$\sqrt{a-1}$<2$\sqrt{a}$.(2)求证:a2+b2≥ab+a+b-1.
分析 (1)利用分析法即可证明结论;
(2)欲证明a2+b2≥ab+a+b-1,利用比较法,只须证明(a2+b2)-(ab+a+b-1)>0即可,故先作差后因式分解后与0比较即可.
解答 证明:(1)要证$\sqrt{a+1}$+$\sqrt{a-1}$<2$\sqrt{a}$,
只需证($\sqrt{a+1}$+$\sqrt{a-1}$)2<(2$\sqrt{a}$)2,
只需证$\sqrt{{a}^{2}-1}$<a,
只需证a2-1<a2,
a2-1<a2,显然成立;(6分)
(2)(a2+b2)-(ab+a+b-1)
=$\frac{1}{2}$(2a2+2b2-2ab-2a-2b+2)
=$\frac{1}{2}$[(a2-2ab+b2)+(a2-2a+1)+(b2-2b+1)]
=$\frac{1}{2}$[(a-b)2+(a-1)2+(b-1)2]≥0,
∴a2+b2≥ab+a+b-1.(12分)
点评 本题考查不等式的证明,考查比较法、分析法的运用,属于中档题.

练习册系列答案
相关题目
5.一个总体中的1000个个体编号为0,1,2,…,999,并以此将其分为10个小组,组号为1,2,3,…,10,要用系统抽样方法抽取一个容量为10的样本,规定如果在第1组抽取的号码为x,那么依次错位地得到后面各组的号码,即第k组中抽取的号码的后两位数为x+33k的后两位数,若x=57,则第7组抽取的号码为( )
| A. | 657 | B. | 757 | C. | 688 | D. | 788 |
3.等差数列{an}中,a1+a2=3,a3+a4=7,则a5+a6=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
10.f(x)是R上的可导函数,且f(x)+xf′(x)>0对x∈R恒成立,则下列恒成立的是( )
| A. | f(x)>0 | B. | f(x)<0 | C. | f(x)>x | D. | f(x)<x |
4.已知向量$\vec a$=(1,2),$\vec b$=(k+1,3),若$\vec a$与$\vec b$的夹角为锐角,则实数k的取值范围为( )
| A. | (-7,+∞) | B. | (-7,$\frac{1}{2}}$)∪(${\frac{1}{2}$,+∞) | C. | [-7,+∞) | D. | [-7,$\frac{1}{2}}$)∪(${\frac{1}{2}$,+∞) |
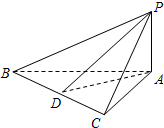 如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.
如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.