题目内容
5.已知数列{an}是各项均为正数有穷数列,数列{bn}满足kbk=a1+a2+…+ak(k=1,2,…,n)(1)若数列{bn}的通项公式bn=n,求数列{an}的通项公式;
(2)①若数列{an}为递增数列,试判断数列{bn}是否为递增数列?如果是,请加以证明;如果不是,说明理由;
②若数列{bn}为递增数列,试判断数列{an}是否为递增数列?如果是,请加以证明;如果不是,说明理由;
(3)设数列{Cn}、{Dn}满足:Cn=(a1-b1)2+(a2-b2)2+…+(an-bn)2,Dn=(a1-bn)2+(a2-bn)2+…+(an-bn)2,求证:Cn≤Dn.
分析 (1)运用递推关系式kbk=a1+a2+…+ak(k=1,2,…,n),得出(n-1)(n-1)=a1+a2+…+an-1,n×n=(a1+a2+…+an-1+an),求解即可得出an=n2-(n-1)2=2n-1,(n≥2),验证n=1是否满足即可.
(2)(i)作差得出bn+1-bn=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}+{a}_{n+1}}{n+1}$-$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$=$\frac{n{a}_{n+1}-({a}_{1}+{a}_{2}+…+{a}_{n})}{n(n+1)}$>0,运用数列{an}为递增数列,放缩a1+a2+…+an<nan,nan+1-(a1+a2+…+an)>n(an+1-an)>0可得证.(ii)运用特殊数列论证即可.
(3)作差Dn-Cn=(a1-bn)2+(a2-bn)2+…+(an-bn)2-(a1-b1)2+(a2-b2)2+…+(an-bn)2,由kbk=a1+a2+a3+…+ak,可知ak+1=(k+1)bk+1-kbk,a1=b1,…
利用上式,将Dn-Cn展开,将ai用{bn}的项替换,化简即可得证.
解答 解:(1)∵bn=n,kbk=a1+a2+…+ak(k=1,2,…,n),
∴1×1=a1,
即a1=1,
当k=n-1时,(n-1)(n-1)=a1+a2+…+an-1(n≥2),①
当k=n时,n×n=(a1+a2+…+an-1+an②
②-①得出an=n2-(n-1)2=2n-1,(n≥2),
当n=1时,也符合式子,
∴数列{an}的通项公式:an=2n-1,
(2)(i)∵数列{an}为递增数列
∴a1+a2+…+an<nan,
∴nan+1-(a1+a2+…+an)>n(an+1-an)>0
∵nbn=a1+a2+…+an(n≥1),
∴bn=$\frac{{a}_{1}+{a}_{2}+++{a}_{n}}{n}$,①
可得bn+1=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}+{a}_{n+1}}{n+1}$,②
②-①得出:bn+1-bn=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}+{a}_{n+1}}{n+1}$-$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$
=$\frac{n{a}_{n+1}-({a}_{1}+{a}_{2}+…+{a}_{n})}{n(n+1)}$>0,
即bn+1>bn,
∴数列{an}为递增数列,可以判断数列{bn}是递增数列.
(ii)当数列{bn}为1,5,6时,{an}为1,9,8,
所以若数列{bn}为递增数列,试判断数列{an}不为递增数列.
(3)证明:Dn-Cn=(a1-bn)2+(a2-bn)2+…+(an-bn)2-(a1-b1)2+(a2-b2)2+…+(an-bn)2,
由kbk=a1+a2+a3+…+ak,可知ak+1=(k+1)bk+1-kbk,a1=b1,…
利用上式,将Dn-Cn展开,将ai用{bn}的项替换,得出:
Dn-Cn=(b1-b2)2+2(b2-b3)2+…+(n-1)(bn-1-bn)2≥0,
∴Dn≥Cn
点评 本题综合考察了数列的知识,性质,结合不等式,放缩法求解,难度较大,考察了学生的化简运算能力,分析解决问题的能力.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 2ab-1-a2b2≤0 | B. | ${a^2}+{b^2}-1-\frac{{{a^4}+{b^4}}}{2}≤0$ | ||
| C. | $\frac{{{{(a+b)}^2}}}{2}-1-{a^2}{b^2}≤0$ | D. | (a2-1)(b2-1)≥0 |
| A. | (-$\sqrt{6}$,$\sqrt{6}$) | B. | (-$\frac{\sqrt{2}}{3}$,$\frac{\sqrt{2}}{3}$) | C. | (-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) |
| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 2$\root{4}{3}$ |
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
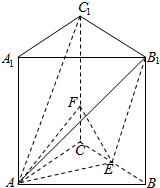 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=BC=AC=AA1=4,点F在CC1上,且C1F=3FC,E是BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=BC=AC=AA1=4,点F在CC1上,且C1F=3FC,E是BC的中点.