题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,讨论
时,讨论![]() 极值点的个数;
极值点的个数;
(2)若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)极大值点![]() ,且是唯一极值点;(2)
,且是唯一极值点;(2)![]()
【解析】
(1)将![]() 代入,求导得到
代入,求导得到![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,进而可判断出
,进而可判断出![]() 是
是![]() 的极大值点,且是唯一极值点;
的极大值点,且是唯一极值点;
(2)令![]() ,得到
,得到![]() ,则
,则![]() 与
与![]() 的图象在
的图象在![]() 上有2个交点,利用导数,数形结合即可得到
上有2个交点,利用导数,数形结合即可得到![]() 的取值范围.
的取值范围.
解:(1)由![]() 知
知![]() .
.
当![]() 时,
时,![]() ,
,![]() ,显然
,显然![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() ,
,
∴![]() 在
在![]() 上存在零点
上存在零点![]() ,且是唯一零点,
,且是唯一零点,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() 是
是![]() 的极大值点,且是唯一极值点.
的极大值点,且是唯一极值点.
(2)令![]() ,则
,则![]() .
.
令![]() ,
,![]() ,
,
则![]() 和
和![]() 的图象在
的图象在![]() 上有两个交点,
上有两个交点,
 .
.
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,而
上单调递减,而![]() ,
,
故当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递减.
单调递减.
故![]() .
.
又![]() ,当
,当![]() 且
且![]() 时,
时,![]() 且
且![]() ,
,
结合图象,可知若![]() 和
和![]() 的图象在
的图象在![]() 上有两个交点,只需
上有两个交点,只需![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.

【题目】某生鲜超市每天从蔬菜生产基地购进某种蔬菜,每天的进货量相同,进价6元/千克,售价9元/千克,当天未售出的蔬菜被生产基地以2元/千克的价格回收处理.该超市发现这种蔬菜每天都有剩余,为此整理了过往30天这种蔬菜的日需求量![]() (单位:千克),得到如下统计数据:
(单位:千克),得到如下统计数据:
日需求量 | 160 | 170 | 180 | 190 | 200 | 210 | 220 |
天数 | 3 | 6 | 6 | 9 | 4 | 1 | 1 |
以这30天记录的各日需求量的频率作为各日需求量的概率,假设各日需求量相互独立.
(1)求在未来的3天中,至多有1天的日需求量不超过190千克的概率;
(2)超市为了减少浪费,提升利润,决定调整每天的进货量![]() (单位:千克),以销售这种蔬菜的日利润的期望值为决策依据,在
(单位:千克),以销售这种蔬菜的日利润的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
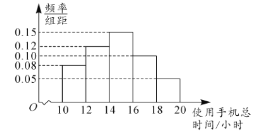
【题目】某单位为了更好地应对新型冠状病毒肺炎疫情,对单位的职工进行防疫知识培训,所有职工选择网络在线培训和线下培训中的一种方案进行培训.随机抽取了140人的培训成绩,统计发现样本中40个成绩来自线下培训职工,其余来自在线培训的职工,并得到如下统计图表:

(1)写出线下培训茎叶图中成绩的中位数,估算在线培训直方图的中位数(保留一位小数);
(2)得分90分及以上为成绩优秀,完成下边列联表,并判断是否有![]() 的把握认为成绩优秀与培训方式有关?
的把握认为成绩优秀与培训方式有关?
优秀 | 非优秀 | 合计 | |
线下培训 | |||
在线培训 | |||
合计 |
附: .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某工厂改造一废弃的流水线M,为评估流水线M的性能,连续两天从流水线M生产零件上随机各抽取100件零件作为样本,测量其直径后,整理得到下表:记抽取的零件直径为X.
第一天
直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
第二天
直径/mm | 58 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 2 | 4 | 5 | 21 | 34 | 21 | 3 | 3 | 2 | 1 | 1 | 1 | 100 |
经计算,第一天样本的平均值![]() ,标准差
,标准差![]() 第二天样本的平均值
第二天样本的平均值![]() ,标准差
,标准差![]()
(1)现以两天抽取的零件来评判流水线M的性能.
(i)计算这两天抽取200件样本的平均值![]() 和标准差
和标准差![]() (精确到0.01);
(精确到0.01);
(ii)现以频率值作为概率的估计值,根据以下不等式进行评判(P表示相应事件的概率),①![]() ;②
;②![]() ;③
;③![]() 评判规则为:若同时满足上述三个不等式,则设备等级为优;仅满足其中两个,则等级为良;若仅满足其中一个,则等级为合格;若全部不满足,则等级为不合格,试判断流水线M的性能等级.
评判规则为:若同时满足上述三个不等式,则设备等级为优;仅满足其中两个,则等级为良;若仅满足其中一个,则等级为合格;若全部不满足,则等级为不合格,试判断流水线M的性能等级.
(2)将直径X在![]() 范围内的零件认定为一等品,在
范围内的零件认定为一等品,在![]() 范围以外的零件认定为次品,其余认定为合格品.现从200件样本除一等品外的零件中抽取2个,设
范围以外的零件认定为次品,其余认定为合格品.现从200件样本除一等品外的零件中抽取2个,设![]() 为抽到次品的件数,求
为抽到次品的件数,求![]() 分布列及其期望.
分布列及其期望.
附注:参考数据:![]() ,
,![]() ,
,![]() ;
;
参考公式:标准差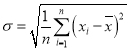 .
.