题目内容
【题目】已知函数![]() ,a为常数.
,a为常数.
(1)讨论函数![]() 的单调性:
的单调性:
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() 且
且![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析(2)证明见解析
【解析】
(1)求导后![]() 分子所对应的二次函数
分子所对应的二次函数![]() ,分情况讨论
,分情况讨论![]() 的正负以及根与1的大小关系即可.
的正负以及根与1的大小关系即可.
(2)由(1)的两个极值点![]() ,
,![]() 满足
满足![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() ,将
,将![]() 化简整理为
化简整理为![]() 的函数即
的函数即![]() ,构造函数求导证明不等式即可.
,构造函数求导证明不等式即可.
(1)函数的定义城为![]() .
.
由题意,![]() .
.
(ⅰ)若![]() ,则
,则![]() ,于是
,于是![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减.
单调递减.
(ⅱ)若![]() ,由
,由![]() ,得
,得![]() 或
或![]() ,
,
当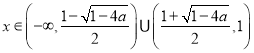 时,
时,![]() ;
;
当 时,
时,![]() ;
;
所以![]() 在
在 ,
,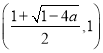 单调递减,
单调递减,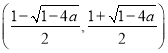 单调递增.
单调递增.
(ⅲ)若![]() ,则
,则![]() ,
,
当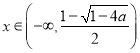 时,
时,![]() ;当
;当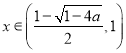 时,
时,![]() ;
;
所以![]() 在
在 单调递减,
单调递减,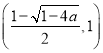 单调递增
单调递增
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在
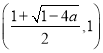 上单调递减,
上单调递减,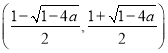 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在 上单调递减,
上单调递减,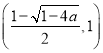 上单调递增.
上单调递增.
(2)由(1)知,![]() 有两个极值点当且仅当
有两个极值点当且仅当![]() .
.
由于![]() 的两个极值点
的两个极值点![]() ,
,![]() 满足
满足![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() ,
,
由于![]() .
.
设![]()
![]() .
.
![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 上单调递减,又
上单调递减,又![]() .
.
所以![]() ,即
,即![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() 年至
年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)

