题目内容
【题目】椭圆![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的弦长为
轴垂直的直线被椭圆截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可知点 在椭圆
在椭圆![]() 上,利用椭圆的定义可求得
上,利用椭圆的定义可求得![]() 值,结合
值,结合![]() 的值可求得
的值可求得![]() 的值,进而可求得椭圆
的值,进而可求得椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 、
、![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,由
的方程联立,列出韦达定理,由![]() 得出
得出![]() ,结合韦达定理求得
,结合韦达定理求得![]() 的值,再由三角形的面积公式可求得
的值,再由三角形的面积公式可求得![]() 的面积.
的面积.
(1)依题意有![]() ,椭圆
,椭圆![]() 的焦点坐标为
的焦点坐标为![]() ,且点
,且点 在椭圆
在椭圆![]() 上,
上,
由椭圆的定义可得 ,
,
即![]() ,
,![]() ,
,
因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)设![]() 、
、![]() ,由
,由![]() ,得
,得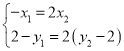 .
.
由题意直线![]() 的斜率存在,所以设直线
的斜率存在,所以设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程整理,得![]() ,
,
所以![]() ,
,![]() .
.
将![]() 代入上式可得,
代入上式可得,![]() ,解得
,解得![]() .
.
所以![]() 的面积
的面积
![]() .
.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案【题目】某市教育局为了监控某校高一年级的素质教育过程,从该校高一年级16个班随机抽取了16个样本成绩,制表如下:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
测评成绩 | 95 | 96 | 96 | 90 | 95 | 98 | 98 | 97 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
测评成绩 | 97 | 95 | 96 | 98 | 99 | 96 | 99 | 96 |
令![]() 为抽取的第
为抽取的第![]() 个学生的素质教育测评成绩,
个学生的素质教育测评成绩,![]() ,经计算得
,经计算得![]() ,
,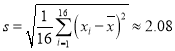 ,
, ,
,![]() ,以下计算精确到0.01.
,以下计算精确到0.01.
(1)求![]() 的相关系数
的相关系数![]() ,并回答
,并回答![]() 与
与![]() 是否可以认为具有较强的相关性;
是否可以认为具有较强的相关性;
(2)在抽取的样本成绩中,如果出现了在![]() 之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议,从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议,从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
附:样本![]() 的相关系数
的相关系数 ,若
,若![]() ,则可以认为两个变量具有较强的线性相关性.
,则可以认为两个变量具有较强的线性相关性.
【题目】某公司有l000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族”,计划在明年及明年以后才购买5G手机的员工称为“观望者”调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(Ⅰ)完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该公司员工属于“追光族”与“性别”有关;
的把握认为该公司员工属于“追光族”与“性别”有关;
属于“追光族” | 属于“观望者” | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(Ⅱ)已知被抽取的这l00名员工中有6名是人事部的员工,这6名中有3名属于“追光族”现从这6名中随机抽取3名,求抽取到的3名中恰有1名属于“追光族”的概率.
附: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |