题目内容
17.已知数列{an}中,an+1=Sn-n+3,n∈N*,a1=2.(1)求证:当n≥2时,n∈N*时,{an-1}是等比数列;
(2)求数列{an}的通项公式;
(3)设bn=$\frac{n}{{S}_{n}-n+2}$(n∈N*)的前n项和为Tn.求证:$\frac{1}{3}≤{T}_{n}<\frac{4}{3}$(n∈N*).
分析 (1)根据等比数列的定义即可证明:当n≥2,n∈N*时,{an-1}是等比数列;
(2)利用{an-1}是等比数列,即可求{an}的通项公式;
(3)化简bn=$\frac{n}{{S}_{n}-n+2}$(n∈N*)运用错位相减法求Tn,再由不等式的性质可得:$\frac{1}{3}$≤Tn<$\frac{4}{3}$(n∈N*).
解答 (1)证明:∵$\left\{\begin{array}{l}{{a}_{n+1}={S}_{n}-n+3}\\{{a}_{n}={S}_{n-1}-(n-1)+3}\end{array}\right.$,(n≥2),
∴an+1-an=an-1⇒an+1-1=2(an-1),
∴{an-1}从第二项起为公比等于2的等比数列.
(2)解:∵{an-1}从第二项起为公比等于2的等比数列.
∴a2=S1-1+3=4,a1=2a2-1≠2(a1-1),
∴an=$\left\{\begin{array}{l}{2,n=1}\\{3•{2}^{n-2}+1,n≥2}\end{array}\right.$.
(3)证明:由(2)知Sn=an+1+n-3=3×2n-1+n-2⇒bn=$\frac{n}{3•{2}^{n-1}}$,
则Tn=$\frac{1}{3}$+$\frac{2}{3•2}$+$\frac{3}{3•{2}^{2}}$+$\frac{4}{3•{2}^{3}}$+…+$\frac{n}{3•{2}^{n-1}}$,
$\frac{1}{2}$Tn=$\frac{1}{3•2}$+$\frac{2}{3•{2}^{2}}$+$\frac{3}{3•{2}^{3}}$+$\frac{4}{3•{2}^{4}}$+…+$\frac{n}{3•{2}^{n}}$,
两式相减得$\frac{1}{2}$Tn=$\frac{1}{3}+$$\frac{1}{3•2}$+$\frac{1}{3•{2}^{2}}$+$\frac{1}{3•{2}^{3}}$+…+$\frac{1}{3•{2}^{n-1}}$-$\frac{n}{3•{2}^{n}}$
=$\frac{1}{3}$($\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$)--$\frac{n}{3•{2}^{n}}$,
即Tn=$\frac{4}{3}$-$\frac{n+2}{3•{2}^{n-1}}$,
∵bn>0,Tn≥T1=$\frac{1}{3}$,又Tn<$\frac{4}{3}$.
∴$\frac{1}{3}≤{T}_{n}<\frac{4}{3}$(n∈N*).
点评 本题主要考查等比数列的应用,以及考查数列求通项、错位相减法求和,考查学生的计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $±\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{8}{9}$ | B. | $\frac{1}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{4}{9}$ |
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{25}$ | p1 | p2 | p3 | p4 |
(Ⅱ)求随机变量ξ的数学期望.
 已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1
已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1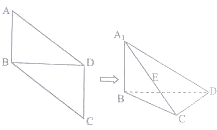 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.