题目内容
【题目】在平面直角坐标系xOy中,已知点A(0,﹣2),B(4,0),圆C经过点(0,﹣1),(0,1)及(![]() ,0).斜率为k的直线l经过点B.
,0).斜率为k的直线l经过点B.
(1)求圆C的标准方程;
(2)当k=2时,过直线l上的一点P向圆C引一条切线,切点为Q,且满足PQ=![]() ,求点P的坐标;
,求点P的坐标;
(3)设M,N是圆C上任意两个不同的点,若以MN为直径的圆与直线l都没有公共点,求k的取值范围.
【答案】(1)![]() ;(2)P(3,﹣2)或(
;(2)P(3,﹣2)或(![]() ,
,![]() );(3)
);(3)![]() 或
或![]() .
.
【解析】
(1)设圆的一般方程,将三个点坐标代入,即得结果,再配方化为标准方程;
(2)设P(x,y),根据切线长以及两点间距离公式列方程,再根据点P在直线上。联立方程组解得结果;
(3)根据垂径定理列出以MN为直径的圆上点满足的条件(一个实心圆),再根据直线与圆位置关系列不等式解得结果.
(1)设圆C的方程为![]() ,
,
因为圆C经过点(0,﹣1),(0,1)及(![]() ,0)
,0)
所以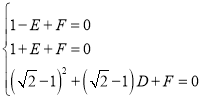 ,解得
,解得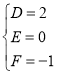 ,
,
所以圆C的方程为:![]() ,其标准方程为
,其标准方程为![]() ,
,
(2)设P(x,y),由PQ与圆C切于点Q,得PQ2=PC2﹣CQ2,又PQ=![]() PA,
PA,
所以![]() ,整理得
,整理得![]() ,
,
又点P在直线l:![]() 上,
上,
由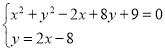 ,得
,得![]() 或
或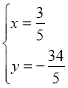
所以P(3,﹣2)或(![]() ,
,![]() ),
),
(3)设以MN为直径的圆的圆心为K,T是该圆上任意一点
则K为MN中点,设CK=d,则圆K的半径为![]()
因为![]() ,所以
,所以![]() ,
,
因为M,N是圆C上任意两个不同的点,所以d∈[0,![]() ),
),
对于任意d∈[0,![]() ),
),![]() ,所以0≤CT2≤4,
,所以0≤CT2≤4,
故点T总在以C(﹣1,0)为圆心,2为半径的圆上或其内部,
故直线l:y=k(x﹣4),即kx﹣y﹣4k=0,与该圆无公共点,
所以![]() ,解得
,解得![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某企业共有员工10000人,下图是通过随机抽样得到的该企业部分员工年收入(单位:万元)频率分布直方图.
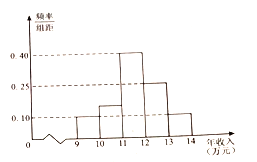
(1)根据频率分布直方图计算样本的平均数.并以此估算该企业全体员工中年收入不低于样本平均数的人数(同一组中的数据以这数据所在区间中点的值作代表);
(2)若抽样调查中收入在![]() 万元员工有2人,求在收入在
万元员工有2人,求在收入在![]() 万元的员工中任取3人,恰有2位员工收入在
万元的员工中任取3人,恰有2位员工收入在![]() 万元的概率;
万元的概率;
(3)若抽样调查的样本容量是400人,在这400人中:年收入在![]() 万元的员工中具有大学及大学以上学历的有
万元的员工中具有大学及大学以上学历的有![]() ,年收入在
,年收入在![]() 万元的员工中不具有大学及大学以上学历的有
万元的员工中不具有大学及大学以上学历的有![]() ,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有
,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有![]() 的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
具有大学及大学以上学历 | 不具有大学及大学以上学历 | 合计 | |
| |||
| |||
合计 |
附:![]() ;
;
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】新冠肺炎疫情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查.已知该校高一年级共有学生660人,抽取的样本中高二年级有50人,高三年级有45人.下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:h)的频率分布表.
分组 | 频数 | 频率 |
| 5 | 0.10 |
| 8 | 0.16 |
| x | 0.14 |
| 12 | y |
| 10 | 0.20 |
| z | |
合计 | 50 | 1 |
(1)求该校学生总数;
(2)求频率分布表中实数x,y,z的值;
(3)已知日睡眠时间在区间[6,6.5)的5名高二学生中,有2名女生,3名男生,若从中任选2人进行面谈,则选中的2人恰好为一男一女的概率.