题目内容
【题目】已知圆C经过A（﹣2，1），B（5，0）两点，且圆心C在直线y=2x上．
（1）求圆C的方程；
（2）动直线l：（m+2）x+（2m+1）y﹣7m﹣8=0过定点M，斜率为1的直线m过点M，直线m和圆C相交于P，Q两点，求PQ的长度．
【答案】
（1）解：设圆C的方程为x2+y2+Dx+Ey+F=0，
则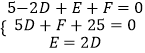 
，
解得D=﹣4，E=﹣8，F=﹣5，
∴圆C的方程：x2+y2﹣4x﹣8y﹣5=0
（2）解：动直线l的方程为（x+2y﹣7）m+2x+y﹣8=0．
则 
得 
，∴动直线l过定点M（3，2），
∴直线m：y=x﹣1，
∴圆心C（2，4）到m的距离为 
，
∴PQ的长为 
【解析】（1）先设出圆的一般方程，再将所给的圆上点的坐标及圆心的关系代入即可求得圆的一般方程；（2）先根据直线l特征求得其定点M的坐标，再结合题意求得直线m的方程，再利用圆心C到直线m的距离、线段PQ的一半及圆C的半径组成的直角三角形求得线段PQ的长.
【考点精析】通过灵活运用直线与圆的三种位置关系，掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点即可以解答此题．
练习册系列答案
相关题目
