题目内容
动点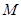 的坐标
的坐标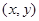 在其运动过程中
在其运动过程中
总满足关系式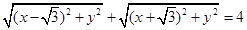 .
.
(1)点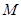 的轨迹是什么曲线?请写出它的标准方程;
的轨迹是什么曲线?请写出它的标准方程;
(2)已知直线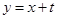 与
与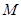 的轨迹交于A、B两点,且OA⊥OB(O为原点),求
的轨迹交于A、B两点,且OA⊥OB(O为原点),求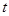 的值.
的值.
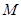 的坐标
的坐标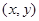 在其运动过程中
在其运动过程中总满足关系式
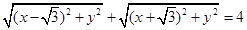 .
.(1)点
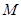 的轨迹是什么曲线?请写出它的标准方程;
的轨迹是什么曲线?请写出它的标准方程;(2)已知直线
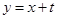 与
与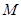 的轨迹交于A、B两点,且OA⊥OB(O为原点),求
的轨迹交于A、B两点,且OA⊥OB(O为原点),求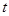 的值.
的值.(1)(6分)椭圆: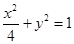
(2)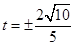
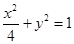
(2)
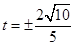
分析:(1)根据
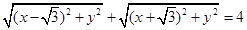 ,可得(x,y)与(-
,可得(x,y)与(-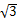 ,0),(
,0),(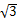 ,0)的距离之和等于常数4,由椭圆的定义可知点M的轨迹,从而可得椭圆的方程;
,0)的距离之和等于常数4,由椭圆的定义可知点M的轨迹,从而可得椭圆的方程;(2)直线y=x+t与M的轨迹方程联立,消去y,利用韦达定理及OA⊥OB,即可求得t的值。
解答:
(1)∵
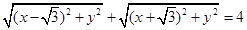
∴(x,y)与(-
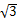 ,0),(
,0),(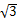 ,0)的距离之和等于常数4,
,0)的距离之和等于常数4,由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且a=2,c=
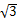 ,
,∴b=1,故椭圆的方程为:x2/4+y2=1;
(2)直线y=x+t与M的轨迹方程联立,消去y可得5x2+8tx+4t2-4=0
设A(x1,y1),B(x2,y2),则x1+x2=-8t/5,x1x2=(4t2-4)/5,
∴y1y2=(x1+t)(x2+t)=-4/5+1/5t2
∵OA⊥OB
∴x1x2+y1y2=(4t2-4)/5-4/5+1/5t2=0
∴
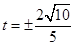
点评:本题考查轨迹方程,考查直线与椭圆的位置关系,求得椭圆的方程,正确运用韦达定理是关键。

练习册系列答案
相关题目
 •
• 的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.
的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值. 倍后得到点Q(x,
倍后得到点Q(x,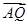 ·
·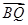 =1.
=1. 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且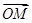 +
+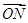 +
+ =
=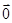 ,试求△MNH的面积.
,试求△MNH的面积.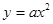 在点(1,
在点(1,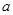 )处的切线与直线
)处的切线与直线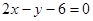 平行,则
平行,则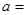 ( )
( )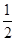
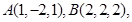 点
点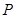 在
在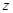 轴上,且
轴上,且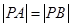 ,则点
,则点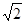 +1,
+1, 为该平面上一动点,作
为该平面上一动点,作 ,垂足为Q,且(
,垂足为Q,且(
 与(1)中的曲线交于不同的两点A、B,是否存在实数k,使得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
与(1)中的曲线交于不同的两点A、B,是否存在实数k,使得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由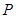 是椭圆
是椭圆 上位于
上位于 轴上方的一点,F是椭圆的左焦点,
轴上方的一点,F是椭圆的左焦点,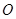 为原点,
为原点,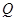 为
为 的中点,且
的中点,且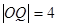 ,则直线
,则直线