题目内容
已知m∈R,直线l:mx-(m2+1)y=4m和圆C:x2+y2-8x+4y+16=0.
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为的两段圆弧?为什么?
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为的两段圆弧?为什么?
解:(1)直线l的方程可化为y=x-,直线l的斜率k=,
因为|m|≤(m2+1),
所以|k|=≤,当且仅当|m|=1时等号成立.
所以斜率k的取值范围是[-,]. …………6分
(2)不能.
由(1)知l的方程为y=k(x-4),其中|k|≤.
圆C的圆心为C(4,-2),半径r=2.
圆心C到直线l的距离d=.
由|k|≤,得d≥>1,即d>.
从而,若l与圆C相交,则圆C截直线l所得的弦所对的圆心角小于.
所以l不能将圆C分割成弧长的比值为的两段弧. …………12分
因为|m|≤(m2+1),
所以|k|=≤,当且仅当|m|=1时等号成立.
所以斜率k的取值范围是[-,]. …………6分
(2)不能.
由(1)知l的方程为y=k(x-4),其中|k|≤.
圆C的圆心为C(4,-2),半径r=2.
圆心C到直线l的距离d=.
由|k|≤,得d≥>1,即d>.
从而,若l与圆C相交,则圆C截直线l所得的弦所对的圆心角小于.
所以l不能将圆C分割成弧长的比值为的两段弧. …………12分
略

练习册系列答案
相关题目
 是单位圆
是单位圆 上的任意一点,
上的任意一点, 是过点
是过点 轴垂直的直线,
轴垂直的直线, 是直线
是直线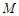 在直线
在直线 . 当点
. 当点 .
. 的直线交曲线
的直线交曲线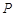 ,
,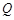 两点,其中
两点,其中 轴上的射影为点
轴上的射影为点 ,直线
,直线 交曲线
交曲线 . 是否存在
. 是否存在 ,使得对任意的
,使得对任意的 ,都有
,都有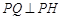 ?若存在,求
?若存在,求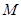 的坐标
的坐标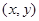 在其运动过程中
在其运动过程中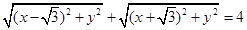 .
.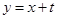 与
与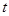 的值.
的值.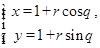 (θ为参数,r >0),若直线l与圆C相切,求r的值.
(θ为参数,r >0),若直线l与圆C相切,求r的值.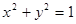 上运动时,它与定点Q(3,0)所连线段PQ的中点M的轨迹方程是:
上运动时,它与定点Q(3,0)所连线段PQ的中点M的轨迹方程是: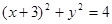
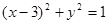
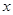 轴正半轴上一点
轴正半轴上一点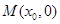 ,作圆
,作圆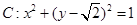 的两条切线,切点分别为
的两条切线,切点分别为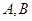 ,若
,若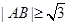 ,则
,则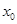 的最小值为( )
的最小值为( )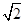
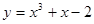 上点
上点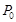 处的切线斜率为4,则点
处的切线斜率为4,则点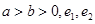 分别是圆锥曲线
分别是圆锥曲线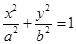 和
和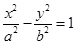 的离心率,设
的离心率,设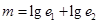 ,则
,则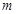 的取值范围是 .
的取值范围是 .