题目内容
3.如图,沿格子型路线从点A到点C,如果只能向右、向上走,则经过点B的概率是$\frac{4}{7}$.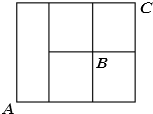
分析 沿格子型路线从点A出发,且只能向右或向上走,到达C点有七种走法,其中经过B点的有四种走法,由此求得经过点B的概率.
解答 解:沿格子型路线从点A出发,且只能向右或向上走,
到达D,E,F,G点只有一种走法;
到达B,H点有两种走法;
到达K点有三种走法;
到达I点有四种走法;
到达C点有七种走法,
其中经过B点的有四种走法,
故经过点B的概率P=$\frac{4}{7}$,
故答案为:$\frac{4}{7}$
点评 本题主要考查古典概型,解决古典概型问题时最有效的工具是列举,要求能通过列举解决古典概型问题,也有一些题目需要借助于排列组合来计数.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
13.A={x|(a-2)x2-2(a-2)x-4<0},若A=R(R为实数集),则实数a的取值范围为( )
| A. | (-2,2) | B. | (-2,+∞) | C. | (-2,2] | D. | ∅ |
8.已知一物体从100米高处落下,若落下的距离h与落下的时间t之间的函数关系式为h=$\frac{1}{2}$gt2,g以10m/s2计,则经过3s后,该物体离地面的高度为( )
| A. | 45米 | B. | 55米 | C. | 70米 | D. | 10米 |
13.已知圆C的方程为x2+y2+2x-8=0,则圆C关于点(1,-2)对称的圆的方程为( )
| A. | (x+2)2+(y+2)2=9 | B. | (x+2)2+(y+2)2=3 | C. | (x-3)2+(y+4)2=9 | D. | (x-3)2+(y+4)2=3 |
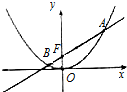 已知抛物线C:y=$\frac{1}{4}$x2,点F(0,1),过点F的直线l交抛物线于A、B两点.
已知抛物线C:y=$\frac{1}{4}$x2,点F(0,1),过点F的直线l交抛物线于A、B两点.