题目内容
14.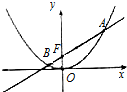 已知抛物线C:y=$\frac{1}{4}$x2,点F(0,1),过点F的直线l交抛物线于A、B两点.
已知抛物线C:y=$\frac{1}{4}$x2,点F(0,1),过点F的直线l交抛物线于A、B两点.(1)若直线l的斜率为1,求A、B的中点坐标和S△OAB;
(2)求△OAB的面积为2,求直线l的方程;
(3)是否存在直线m使得以AB为直径的圆始终与直线m相切.(提示:利用对称性,再画一个圆,猜想出m的位置后再利用特殊圆的位置求出直线m的方程,再证明)
分析 (1)若直线l的斜率为1,则直线l的方程为:y=x+1,联立抛物线方程,根据韦达定理及中点公式,可得A、B的中点坐标,由弦长公式和点到直线距离公式,求出△OAB的底边长和高,可得S△OAB;
(2)设直线l的斜率为k时,△OAB的面积为2,联立直线与抛物线方程,结合弦长公式,及点到直线距离公式,构造关于k的方程,解得答案.;
(3)存在直线y=-1始终与以AB为直径的圆相切,进而利用(2)中结论,求出圆心到直线y=-1的距离等于半径,可得答案.
解答 解:抛物线C:y=$\frac{1}{4}$x2的标准方程为:x2=4y,点F(0,1)为抛物线C的焦点;
(1)若直线l的斜率为1,则直线l的方程为:y=x+1,
代入y=$\frac{1}{4}$x2得$\frac{1}{4}$x2=x+1,
即$\frac{1}{4}$x2-x-1=0,
则设A(x1,y1),B(x2,y2),
则x1+x2=4,x1•x2=-4,
则A、B的中点横坐标为:$\frac{1}{2}$(x1+x2)=2,纵坐标为3,
即A、B的中点坐标为(2,3),
|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{{(x}_{1}+{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$=$\sqrt{2}$×4$\sqrt{2}$=8,
原点O到直线L的距离d=$\frac{1}{\sqrt{1+1}}$=$\frac{\sqrt{2}}{2}$,
故S△OAB=$\frac{1}{2}$|AB|•d=2$\sqrt{2}$,
(2)设直线l的斜率为k时,△OAB的面积为2,
则直线l的方程为:y=kx+1,代入y=$\frac{1}{4}$x2得$\frac{1}{4}$x2=kx+1,
即$\frac{1}{4}$x2-kx-1=0,
则设A(x1,y1),B(x2,y2),
则x1+x2=4k,x1•x2=-4,
|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{{(x}_{1}+{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$=$\sqrt{1+{k}^{2}}$×4$\sqrt{1+{k}^{2}}$=4(l+k2),
原点O到直线L的距离d=$\frac{1}{\sqrt{1+{k}^{2}}}$,
故S△OAB=$\frac{1}{2}$|AB|•d=2$\sqrt{1+{k}^{2}}$=2,
解得:k=0,
此时直线方程为:y=1
(3)存在直线y=-1始终与以AB为直径的圆相切,理由如下:
设直线l的斜率为k,则直线l的方程为:y=kx+1,代入y=$\frac{1}{4}$x2得$\frac{1}{4}$x2=kx+1,
即$\frac{1}{4}$x2-kx-1=0,
则设A(x1,y1),B(x2,y2),
则x1+x2=4k,x1•x2=-4,
则A、B的中点横坐标为:$\frac{1}{2}$(x1+x2)=2k,纵坐标为2k2+1,
|AB|=$\sqrt{1+{k}^{2}}$$\sqrt{{(x}_{1}+{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$=$\sqrt{1+{k}^{2}}$×4$\sqrt{1+{k}^{2}}$=4(l+k2),
故以AB为直径的圆的半径R=$\frac{1}{2}$|AB|=2(l+k2),
而圆心到直线y=-1的距离d=2k2+1-(-1)=2(l+k2),
即存在直线y=-1始终与以AB为直径的圆相切.
点评 本题考查的知识点是抛物线的性质,点到直线的距离公式,弦长公式,三角形面积公式,中点公式,是直线与圆锥曲线的综合应用,难度较大.

| A. | $[{-\frac{3}{2}-\sqrt{2},-\frac{3}{2}+\sqrt{2}}]$ | B. | $[{-\frac{3}{2}-\sqrt{2},\frac{5}{3}}]$ | C. | $[{\frac{3}{2}+\sqrt{2},\frac{5}{3}}]$ | D. | $[{-\frac{10}{3},-\frac{3}{2}-\sqrt{2}}]$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{9}{4}$,$\sqrt{2}$ | B. | $\frac{3}{2}$,$\sqrt{2}$ | C. | $\frac{9}{4}$,$\frac{17}{12}$ | D. | $\frac{9}{4}$,$\frac{3}{2}$ |