题目内容
11.有甲,乙2名男生,4名女生全体排成一行,问下列情形各有多少种不同的排法?(1)甲、乙相邻;
(2)甲、乙互不相邻;
(3)甲不能排在最左端,乙不能排在最右端.
分析 (1)甲、乙相邻,把甲乙两人捆绑在一起看作一个复合元素,再和另外的4名女生全排,问题得以解决;
(2)先排4名女生,形成了5个空,将甲乙插入到其中的2个空中,问题得以解决;
(3)分甲排在最右端或甲不排在最右端,根据分类计数原理得以解决.
解答 解:(1)甲、乙相邻,把甲乙两人捆绑在一起看作一个复合元素,再和另外的4名女生全排,故有A22A55=240种;
(2)先排4名女生,形成了5个空,将甲乙插入到其中的2个空中,故有A44A52=480种;
(3)甲排在最右端,有A55=120种,甲不排在最右端,有A41A41A44=384种,故有120+384=504种.
点评 本题集排列多种类型于一题,充分体现了元素分析法(优先考虑特殊元素)、位置分析法(优先考虑特殊位置)、直接法、捆绑法、插空法等常见的解题思路.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
16.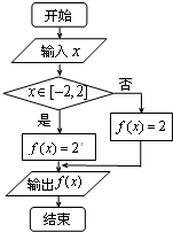 阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )
阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )
 阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )
阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )| A. | (-∞,-2] | B. | (-∞,-2) | C. | [1,+∞) | D. | (-∞,-2)∪[1,+∞) |
1.方程x2+y2+2ax-2ay=0(a≠0)表示的圆( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | ||
| C. | 关于直线x-y=0对称 | D. | 关于直线x+y=0对称 |
 如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.