题目内容
15.已知数列{an}、{bn}满足:a1=4,an+1=$\sqrt{{a}_{n}+2}$,bn=an-1(n∈N*).(1)判断并证明数列{an}的单调性;
(2)是否存在常数λ,使得b1b2b3…bn<λ?若存在,求λ的最小值;若不存在,请说明理由.
分析 (1)由a1=4,an+1=$\sqrt{{a}_{n}+2}$,求得a2,a3,且可知an>0.再由an=$\sqrt{{a}_{n-1}+2}$,两边平方,将n换成n+1,两式作差可得an+1-an与an-an-1同号.由a2-a1的符号,易知,an-an-1<0,即an<an-1,可知数列{an}单调递减;
(2)由an2=an-1+2,可得(an-1)(an+1)=an-1+1,即有an-1=$\frac{{a}_{n-1}+1}{{a}_{n}+1}$,即bn=$\frac{{a}_{n-1}+1}{{a}_{n}+1}$,求得b1b2b3…bn<5,即可判断存在实数λ.
解答 解:(1)数列{an}单调递减.
理由如下:由a1=4,an=$\sqrt{{a}_{n-1}+2}$,
得a2=$\sqrt{6}$,a3=$\sqrt{\sqrt{6}+2}$,且可知an>0.
由an=$\sqrt{{a}_{n-1}+2}$,
得an2=an-1+2①,
则有an+12=an+2②,
由②-①得:an+12-an2=an-an-1,
即(an+1+an)(an+1-an)=an-an-1,
∵an>0,∴an+1-an与an-an-1同号.
由a2-a1=$\sqrt{6}$-4<0,
易知an-an-1<0,即an<an-1,
可知数列{an}单调递减;
(2)∵an2=an-1+2,
∴(an-1)(an+1)=an-1+1,
∴an-1=$\frac{{a}_{n-1}+1}{{a}_{n}+1}$,即bn=$\frac{{a}_{n-1}+1}{{a}_{n}+1}$,
则b1b2b3…bn=3•$\frac{{a}_{1}+1}{{a}_{2}+1}$•$\frac{{a}_{2}+1}{{a}_{3}+1}$…$\frac{{a}_{n-1}+1}{{a}_{n}+1}$
=$\frac{15}{{a}_{n}+1}$.
由(an-2)(an+2)=an-1-2,
易知,an-2与an-1-2同号,
由于a1-2=4-2>0,可知,an-2>0,即an>2,
则$\frac{15}{{a}_{n}+1}$<5,
故存在常数λ,且λ≥5,
对任意n≥2,有b1b2b3…bn<λ成立.
点评 本题是数列与不等式的综合题,考查了数列递推式,训练了累积法求数列的通项公式,训练了放缩法证明数列不等式,属中档题.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 0 |
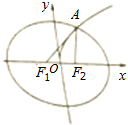 如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.