Question

【题目】已知m，n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（　　）
A.mα，nα，m∥β，n∥βα∥β
B.α∥β，mα，nβ，m∥n
C.m⊥α，m⊥nn∥α
D.m∥n，n⊥αm⊥α

Answer 1

【答案】D
【解析】解：在长方体ABCD﹣A1B1C1D1中，
A、若平面AC是平面α，平面BC1是平面β，
直线AD是直线m，点E，F分别是AB，CD的中点，则EF∥AD，EF是直线n，
显然满足α∥β，mα，nβ，但是m与n异面；
B、若平面AC是平面α，平面A1C1是平面β，
直线AD是直线m，A1B1是直线n，
显然满足mα，nα，m∥β，n∥β，但是α与β相交；
C、若平面AC是平面α，直线AD是直线n，AA1是直线m，
显然满足m⊥α，m⊥n，但是n∈α；
故选D．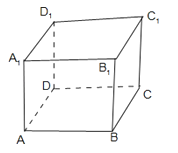

【考点精析】通过灵活运用空间中直线与平面之间的位置关系，掌握直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点即可以解答此题．