Question

【题目】（Ⅰ）设不等式对满足的一切实数的取值都成立，求的取值范围；

（Ⅱ）是否存在实数,使得不等式对满足的一切实数的取值都成立．

Answer 1

【答案】（I）；（II）见解析.

【解析】试题分析：（1）不等式可视为关于m的一次函数，根据一次函数单调性可得方程组，解方程组可得的取值范围；（2）显然不等式为二次不等式时才有满足条件的解，根据二次函数实根分布列方程组，解得方程组可得实数范围为空集

试题解析：（Ⅰ）不等式可化为，

令 ,

要使不等式对满足的一切实数的取值都成立，即只需当时， 恒成立，

关于的函数的图象是一条直线，则有

，即，即

∴满足条件的的取值范围为.

（Ⅱ）令 ，使的一切实数都有.

当时， 在时， ，不满足题意；

当时， 只需满足下式

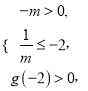或或

解之得上述不等式组的解集均为空集，

故不存在满足条件的的值.