Question

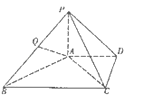
【题目】如图所示的几何体中，四边形ABCD是矩形，平面ABCD⊥平面ABE，已知AB=2，AE=BE= ，且当规定正视图方向垂直平面ABCD时，该几何体的侧视图的面积为 ．若M，N分别是线段DE、CE上的动点，则AM+MN+NB的最小值为

Answer 1

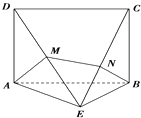
【答案】3
【解析】解：取AB中点F，∵AE=BE= ，∴EF⊥AB， ∵平面ABCD⊥平面ABE，∴EF⊥平面ABCD，
易求EF= ，
左视图的面积S= ADEF= AD= ，
∴AD=1，∴∠AED=∠BEC=30°，∠DEC=60°，
将四棱锥E﹣ABCD的侧面AED、DEC、CEB展开铺平如图，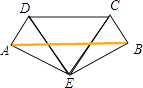

则AB2=AE2+BE2﹣2AEBEcos120°=3+3﹣2×3×（﹣ ）=9，
∴AB=3，
∴AM+MN+BN的最小值为3．
所以答案是：3．
【考点精析】解答此题的关键在于理解由三视图还原实物图的相关知识，掌握正视图：从前往后;侧视图：从左往右;俯视图：从上往下．