题目内容
【题目】某商场举行优惠促销活动，顾客仅可以从以下两种优惠方案中选择一种，
方案一：每满200元减50元；
方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、l个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
（1）若两个顾客都选择方案二，各抽奖一次，求至少一个人获得半价优惠的概率；
（2）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？
【答案】（1）
（2）方案二更为划算
【解析】
（1）设事件
为“顾客获得半价”，可以求出
，然后求出两位顾客都没有获得半价优惠的概率，然后利用对立事件的概率公式，求出两位顾客至少一人获得半价的概率；
（2）先计算出方案一，顾客付款金额，再求出方案二付款金额
元的可能取值，求出
，最后进行比较得出结论.
（1）设事件为“顾客获得半价”，则
，
所以两位顾客至少一人获得半价的概率为：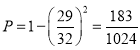
．
（2）若选择方案一，则付款金额为
．
若选择方案二，记付款金额为元，则可取的值为
．
，
，
，
，
∴
．
所以方案二更为划算．
【题目】当前全世界人民越来越关注环境保护问题，某地某监测站点于2018年8月起连续n天监测空气质量指数（AQI），数据统计如下表：
空气质量指数（μg/m3） | [0，50] | （50，100] | （100，150] | （150，200] | （200，250] |
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 | m | 10 | 5 |
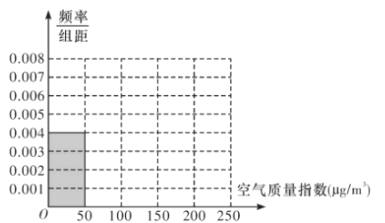
（1）根据所给统计表和频率分布直方图中的信息求出n，m的值，并完成频率分布直方图；
（2）由频率分布直方图，求该组数据的平均数与中位数；
（3）在空气质量指数分别为[0，50]和（50，100]的监测数据中，用分层抽样的方法抽取6天，从中任意选取2天，求事件A“两天空气质量等级都为良”发生的概率。
